时间:2019-07-03 00:01:17
1、计算题 如图所示，一“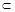
”形绝缘导轨竖直放置，处在水平向右的匀强电场中。左边的半圆弧与水平杆AB、CD相切于A、C两点，两水平杆的高度差为2L，杆AB、CD长度均为4L，O为AD、BC连线的交点，虚线MN、PQ的位置如图，其中AM ="MP" =" CN" =" NQ=" L，PB=QD=2L。虚线MN左边的导轨光滑，虚线MN右边的导轨与小球之间的动摩擦因数为μ。现把一质量为m，电荷量为-q的小球穿在杆上，自N点由静止释放后，小球刚好可到达A点。已知静电力常量为k，重力加速度为g。求
：
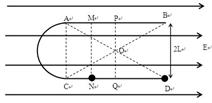
(1) 匀强电场的电场强度E的大小；
（2）小球到达半圆弧中点时，该小球对半圆弧轨道的压力大小；
（3）若在O处固定一点电荷+Q，并将该带电小球自D点以某速度向左瞬间推出，结果小球可沿杆运动到B点。求从D到B点过程中小球所受摩擦力的最大值。
参考答案：(1) E=
?(2) N=8mg (3) fm=μ(mg +
)
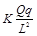本题解析：(1)?小球由N到A过程, 对小球列动能定理：
EqL—2mgL=0? (2分)
E=? (2分)
(2)?小球在圆弧的中点时，由牛顿第二定律得：
N—Eq=m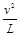
? (2分)
小球由N到圆弧的中点过程中，对小球列动能定理：
Eq(2L)—mgL=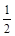
mv2? (2分)
由? E=，得?
N=8mg? (2分)
由牛顿第三定律可知：N=N"=8mg? (1分)
(3)?经分析可知，小球在P点的压力最大，则：
N=mg+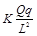? (1分)
fm=μ N? (1分)
fm=μ(mg +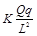)? (1分)
点评：能够分析物体的受力情况和运动情况，选择合适的运动过程运用动能定理求解．动能定理的优点在于适用任何运动包括曲线运动．动能定理的应用范围很广，可以求速度、力、功等物理量，特别是可以去求变力功．
本题难度：一般
2、填空题 A、B两物体各自在甲、乙两处受到一竖直向上的外力作用后，在竖直方向上做变加速直线运动。利用传感器和计算机可以测量快速变化的力与加速度，如图所示是用这种方法获得的物体A、B所受的外力F与加速度a的关系图线，则物体A、B的质量大小关系为mA____________mB，甲、乙两处的重力加速度的关系为gA____________gB（均填写“＞”、“＜”或“＝”）。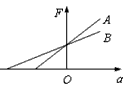 
参考答案：＞，＜
本题解析：
本题难度：一般
3、填空题 某人在地面上最多能举起60kg的物体，则他在以2m/s2的加速度匀加速下降的电梯里最多能举起?kg的物体。（g取10m/s2）
参考答案：75kg
本题解析：某人在地面上最多能举起60kg的物体，所以人的举力F=600N.
在以2m/s2的加速度匀加速下降的电梯里
,解得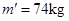
点评：注意本题关键是人的最大举力是一定的。
本题难度：一般
4、计算题 （12分）如图所示，正方形木板水平放置在地面上，木板的中心静置一小滑块。为将木板从滑块下抽出，需要对木板施加一个作用线通过木板中心点的水平恒力F．已知木板边长L=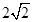
m，质量M= 3kg，滑块质量m=2kg，滑块与木板、木板与地面间的动摩擦因数均为
（取g=10
，设最大静摩擦力等于滑动摩擦力），求：
（1）水平拉力至少多大才能将木板抽出；
（2）当水平恒力F=29N时，在木板抽出时滑块能获得的最大速度．
参考答案：(1)20N? (2)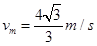 
本题解析：(1)能抽出木板，滑块与木板应相对滑动，当滑块达到随板运动的最大加速度时，拉力最小，
对滑块，有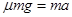
?①?对木板，有
?②
解得：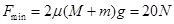
?③?即能抽出木板的最小拉力应大于20N
(2)要使滑块获得的速度最大，则滑块在木板上相对的距离最大，故应沿木板的对角线方向抽木板．⑤
设此时木板加速度为a1，则有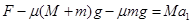
?⑥?又
?⑦
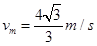?⑧?解得：?⑨
本题难度：一般
5、简答题 一内壁光滑的半环形细圆管竖直地固定在水平桌面上，其直径AB与桌面垂直，环的半径为R（比细管的半径大得多）．一个质量为m的小球（小球直径略小于细管直径且可视为质点）从管口A射入管中，从管口B射出时对管口壁的压力为mg/3．求小球在桌面上的落点到管口A的距离．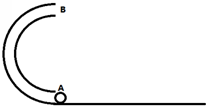
参考答案：当小球在B处所受弹力向上时，小球射出速度为v1，落点到A距离为x1．
由牛顿第二定律得? mg-13mg=mv21R
得v1=
本题解析：
本题难度：一般