时间:2019-07-02 23:59:55
1、选择题 如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉至水平位置,而后释放,摆球运动过程中,支架始终不动.以下说法正确的应是( )
A.在释放瞬间,支架对地面压力为(m+M)g
B.在释放瞬间,支架对地面压力为Mg
C.摆球到达最低点时,支架对地面压力为(m+M)g
D.摆球到达最低点时,支架对地面压力为(3m+M)g
2、选择题 质量为m的物体沿着半径为r的半球形金属球壳滑到最低点时的速度大小为υ,如图所示,若物体与球壳之间的摩擦因数为μ,则物体在最低点时的 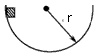
[? ]
A.向心加速度为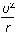
B.向心力为m(g+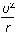 )?
)?
C.对球壳的压力为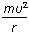 ?
?
D.受到的摩擦力为μm(g+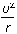 )?
)?
3、填空题 物体因绕轴转动时而具有的动能叫转动动能.转动动能的大小与角速度大小有关,为了探究转动动能的大小与角速度之间的定量关系,某同学设计了下列一个实验,即研究砂轮的转动.先让砂轮由电动机带动作匀速转动并测出其角速度ω,然后让砂轮脱离动力,由于克服轮边缘的摩擦阻力做功,砂轮最后会停下来,测出砂轮开始脱离动力到停止转动的圈数n,实验中得到几组n和ω的数值见下表:(砂轮直径d=10cm,转轴间摩擦力大小?f=
| 1 π |
| n | 5 | 20 | 80 | 180 | 320 ω(rad/s) 0.5 1 2 3 4 Ek(J) ______ ______ ______ ______ ______ |
4、简答题 如图所示的电路中,电源电动势为E,内电阻为r0,滑动变阻器的总电阻3r0,当滑动变阻器的触头P滑到距右端b的距离为总长的
| 1 3 |

5、选择题 如图所示,绳子的一端固定在O点,另一端拴一重物在水平面上做匀速圆周运动( )
A.转速相同时,绳长的容易断
B.周期相同时,绳短的容易断
C.线速度大小相等时,绳短的容易断
D.线速度大小相等时,绳长的容易断