时间:2019-07-02 23:49:37
1、选择题 如图，质量为m的人在质量为M的平板车上从左端走到右端，若不计平板车与地面的摩擦，则下列说法不正确的是（ ）
A．人在车上行走时，车将向左运动
B．当人停止走动时，由于车的惯性大，车将继续后退
C．若人越慢地从车的左端走到右端，则车在地面上移动的距离越大
D．不管人在车上行走的速度多大，车在地面上移动的距离都相同
参考答案：A、人与车组成的系统动量守恒，由动量守恒定律得：mv人+Mv车=0，v车=-mv人M，负号表示人与车的速度方向相反，人在车上向右行走时，车将向左运动，故A正确；
B、由v车=-mv人M可知，人停止走动速度为零时，车的速度也为零，故B错误；
C、车与人的位移之比x车x人v车tv人t=mM=x车x车+L，车的位移x车=mLM-m，L为车的长度，则车的位移与人的运动速度无关，故C错误，D正确；
本题选错误的，故选BC．
本题解析：
本题难度：简单
2、计算题 如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙.重物质量为木板质量的2倍,重物与木板间的动摩擦因数为μ.使木板与重物以共同的速度v0向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短.求木板从第一次与墙碰撞到再次碰撞所经历的时间.设木板足够长,重物始终在木板上.重力加速度为g.
参考答案：
本题解析：木板第一次与墙碰撞后,木板的速度反向,大小不变,此后木板向左做匀减速运动,重物向右做匀减速运动,最后木板和重物达到一共同速度为v,设木板的质量为m,重物的质量为2m,取向右为动量的正向,由动量守恒得
2mv0-mv0=3mv
设从第一次与墙碰撞到木板和重物具有共同速度v所用的时间为t1,
2μmgt1=mv-m(-v0)
由牛顿第二定律得2μmg=ma
式中a为木板的加速度.
在达到共同速度v时,木板离墙的距离l为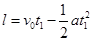
开始向右做匀速运动到第二次与墙碰撞的时间为
从第一次碰撞到第二次碰撞所经过的时间为
t=t1+t2
由以上各式得
本题难度：一般
3、简答题 如图所示，质量为M=4kg的木板放置在光滑的水平面上，其左端放置着一质量为m=2kg的滑块(视作质点)，某时刻起同时给二者施以反向的力，如图，已知F1=6N，F2=3N，
适时撤去两力，使得最终滑块刚好可到达木板右端，且二者同时停止运动，已知力F2在t2=2s时撤去，板长为S=4.5m，g=10m/s2，求
(1)?力F1的作用时间t1
(2)?二者之间的动磨擦因数μ
(3)? t2=2s时滑块m的速度大小
参考答案：（１）t1=1s（２）μ=0.1（３）=1m/s
本题解析：(1)?以向右为正，?对整体的整个过程，由动量定理得?
F1t1-F2t2="0?" 代入数据得t1=1s
(2)?在t1时间内，对m，由F合=ma得? F1-μmg=mam?代入数据可得am=2m/s2
m在t1时间内的位移大小S1=
am t12?代入数据得 S1=1m
同理在t2时间内，对M有? F2-μmg=MaM?代入数据得? aM=0.25m/s2
M在t2时间内的位移大小S2=aM t22?代入数据得 S2=1m
整个过程中，系统的机械能未增加，由功能关系得? F1S1+F2S2-μmgs="0?"
代入数据得μ=0.1
(3) 在t2=2s内，m先加速后减速，撤去F1后，m的加速度大小为
=1m/s2?
所以m在t2=2s时的速度=amt1-
(t2-t1)?代入数据得=1m/s
本题难度：一般
4、计算题 如图所示，半径为r=0.4m的1/4圆形光滑轨道AB固定于竖直平面内，轨道与粗糙的水平地面相切于B点，CDE为固定于竖直平面内的一段内壁光滑的中空方形细管，DE段被弯成以O为圆心、半径R=0.2m的一小段圆弧，管的C端弯成与地面平滑相接，O点位于地面，OE连线竖直．可视为质点的物块b，从A点由静止开始沿轨道下滑，经地面进入细管（b横截面略小于管中空部分的横截面），b滑到E点时受到细管下壁的支持力大小等于所受重力的1/2．已知物块b的质量m = 0.4kg，g取10m/s2．
（1）求物块b滑过E点时的速度大小vE．
（2）求物块b滑过地面BC过程中克服摩擦力做的功Wf．
（3）若将物块b静止放在B点，让另一可视为质点的物块a，从A点由静止开始沿轨道下滑，滑到B点时与b发生弹性正碰，已知a的质量M≥m，求物块b滑过E点后在地面的首次落点到O点的距离范围．
参考答案：(1)1m/s(2) 
(3) 0.2m≤x＜1m
本题解析：（1）物块b滑过E点时重力和支持力的合力提供向心力，根据牛顿第二定律得
（2分）代入 
联立解得 
（1分）
（2）物块b从A点到E点的过程中，由动能定理得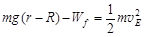
（2分）
解得 （1分）
（3）物块a从A滑到B的过程机械能守恒，设物块a滑到B点时速度为v，则有
（1分）
解得 
设碰撞后物块a、b的速度分别为va、vb，碰撞过程由动量守恒和机械能守恒得
（2分）
（2分）
联立解得 
因为M≥m，由上式可知，
碰撞后v≤vb＜2v，即
m/s≤vb＜
m/s （2分）
物块b从B点到E点的过程中，由动能定理得
（2分）
物块b离开E点后做平抛运动，设时间为t，首次落点到O点的距离为x，则有
（1分）
（1分）
由以上三式联立解得 0.2m≤x＜1m（1分）
考点：考查了动量守恒，机械能守恒，牛顿第二定律，平抛运动，动能定理，圆周运动
本题难度：困难
5、计算题 某同学利用如图所示的装置验证动量守恒定律。图中两摆摆长相同，悬挂于同一高度，A、B两摆球均很小，质量之比为1∶2。当两摆均处于自由静止状态时，其侧面刚好接触。向右上方拉动B球使其摆线伸直并与竖直方向成45°角，然后将其由静止释放。结果观察到两摆球粘在一起摆动，且最大摆角成30°。若本实验允许的最大误差为±4％（P1、P2分别为两球作用前、后的动量），请论证此实验是否成功地验证了动量守恒定律？ 
参考答案：解：设摆球A、B的质量分别为mA、mB，摆长为l，B球的初始高度为h1，碰撞前B球的速度为vB。在不考虑摆线质量的情况下，根据题意及机械能守恒定律得
①?
?②
设碰撞前、后两摆球的总动量的大小分别为P1、P2。
有P1=mBvB ③
联立①②③式得
④
同理可得
⑤
联立④⑤式得
⑥
代入已知条件得
⑦
由此可以推出
≤4%。
本题解析：
本题难度：一般