时间:2019-07-02 23:47:32
1、计算题 (14分)如图所示,图中左边有一对平行金属板,两板相距为d,电压为U。两板之间有匀强磁场,磁感应强度大小为B0,方向与金属板面平行并垂直于纸面朝里;图中右边有一半径为R、圆心为O的圆形区域,区域内也存在匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。一电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入平行金属板之间,沿同一方向射出平行金属板之间的区域,并沿直径PQ方向射入磁场区域,最后从圆形区域边界上的G点射出,已知弧QG所对应的圆心角为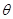 。离子重力不计。求:
。离子重力不计。求: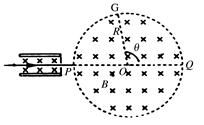
(1)离子速度的大小;
(2)离子在圆形磁场区域内做圆周运动的半径;
(3)离子的质量。
参考答案:(1)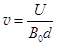 (2)
(2)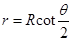 (3)
(3)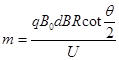
本题解析:(1)粒子匀速运动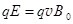 ?(3分)?
?(3分)?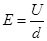 ?(2分) 联立解得:
?(2分) 联立解得: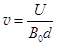 ?(1分)
?(1分)
(2)由几何关系可知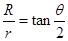 ?(3分)?则离子运动半径
?(3分)?则离子运动半径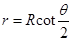 ?(1分)
?(1分)
(3)由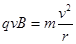 ?(3分)?得
?(3分)?得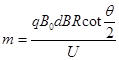 ?(1分)
?(1分)
本题难度:一般
2、选择题 如图所示,匀强电场竖直向上,匀强磁场水平向外,有一正离子(不计重力)恰能沿直线从左向右水平飞越此区域,这种装置称为速度选择器,则( )
A.若电子从左向右水平飞入,电子也沿直线运动
B.若电子从右向左水平飞入,电子将向上偏转
C.若电子从右向左水平飞入,电子将向下偏转
D.若电子从右向左水平飞入,电子将向外偏转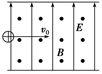
参考答案:AC
本题解析:正电子从左边进入电场,在电场中受到向上的电场力和向下的洛伦兹力作用,因恰能沿直线从左边水平飞出,可知电场力和洛伦兹力平衡,有qE=qv0B,得v0=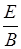 .若粒子带负电,也从左边以速度v0射入,电场力和洛伦兹力的方向对调,发现还是有v0=
.若粒子带负电,也从左边以速度v0射入,电场力和洛伦兹力的方向对调,发现还是有v0=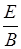 ,所以带电粒子只要以速度v0从左边水平进入电场,粒子就会沿水平方向射出,与电性和电量无关.所以选项A正确,选项B错误.电子从右侧进入电场,受到的电场力方向向下,由左手定则可知,洛伦兹力方向也向下,所以电子将向下偏转.选项C正确,选项D错误.
,所以带电粒子只要以速度v0从左边水平进入电场,粒子就会沿水平方向射出,与电性和电量无关.所以选项A正确,选项B错误.电子从右侧进入电场,受到的电场力方向向下,由左手定则可知,洛伦兹力方向也向下,所以电子将向下偏转.选项C正确,选项D错误.
故选AC.
本题难度:一般
3、计算题 如图所示,x轴的上方存在方向与x轴成45°角的匀强电场,电场强度为E,x轴的下方存在垂直纸面向里的匀强磁场,磁感应强度B=0.5 T。有一个质量m=10-11 kg,电荷量q=10-7 C的带正电粒子,该粒子的初速度v0=2×103 m/s,从坐标原点O沿与x轴成45°角的方向进入匀强磁场,经过磁场和电场的作用,粒子从O点出发后第四次经过x轴时刚好又回到O点处,设电场和磁场的区域足够宽,不计粒子重力,求:
(1)带电粒子第一次经过x轴时的横坐标是多少?
(2)电场强度E的大小及带电粒子从O点出发到再次回到O点所用的时间。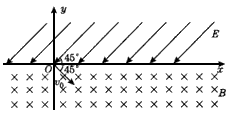
参考答案:解:(1)粒子在磁场中受磁场力的作用沿圆弧运动,洛伦兹力提供向心力qvB=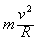
半径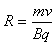 =0.4m
=0.4m
根据圆的对称性可得粒子在磁场中第一次偏转所对的圆心角90°,则第一次经过x轴时的横坐标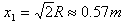 ?
?
(2)粒子第一次进入电场,运动方向与电场方向相反,做匀减速直线运动,速度减为零后又反向加速返回磁场,在磁场中沿圆周运动,再次进入电场时速度方向刚好垂直电场方向,在电场力的作用下偏转,打在坐标原点O处,其运动轨迹如图所示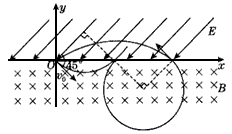
由几何关系可得
第二次进入电场中的位移为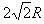
在垂直电场方向的位移s1=vt1
运动时间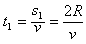 =4×10-4 s
=4×10-4 s
在沿电场方向上的位移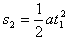
又因s2=2R
得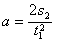 =1×107 m/s2
=1×107 m/s2
根据牛顿第二定律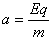
所以电场强度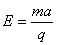 =1×103 V/m
=1×103 V/m
粒子从第一次进入电场到再返回磁场的时间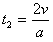 =4×10-4 s
=4×10-4 s
粒子在磁场中两段运动的时间之和刚好做一个完整圆周运动的周期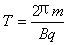 =4π×10-4 s
=4π×10-4 s
所以粒子从出发到再回到原点所用的时间为t=t1+t2+T≈2.1×10-3 s
本题解析:
本题难度:困难
4、选择题 如图所示,两平行金属板中间有相互正交的匀强电场和匀强磁场,电场强度为E,磁感应强度为B,一质子沿极板方向以速度v0从左端射入,并恰好从两板间沿直线穿过。不计质子重力,下列说法正确的是?(?)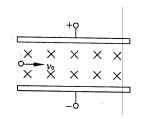
A.若质子以小于v0的速度沿极板方向从左端射入,它将向上偏转
B.若质子以速度2v0沿极板方向从左端射入,它将沿直线穿过
C.若电子以速度v0沿极板方向从左端射入,它将沿直线穿过
D.若电子以速度v0沿极板方向从左端射入,它将沿直线穿过
参考答案:C
本题解析:略
本题难度:一般
5、计算题 如图所示,匀强电场方向水平向右,匀强磁场方向垂直于纸面向里。一质量为m、带电量为q的微粒以速度υ与磁场垂直、与电场成θ角射入复合场中,恰能做匀速直线运动。求电场强度E和磁感应强度B的大小。
参考答案: ?
?
本题解析:微粒受力如图,根据平衡条,得
 ?①
?① ?②
?②
由①②式联立,得

点评:此题关键粒子恰能做匀速直线运动,受力平衡,必考虑重力;对粒子正确进行受力分析,由平衡条件列方程求解。
本题难度:一般