时间:2019-07-02 23:40:19
1、计算题 （18分）有人设计了一种带电颗粒的速率分选装置，其原理如题24图所示，两带电金属板间有匀强电场，方向竖直向上，其中PQNM矩形区域内还有方向垂直纸面向外的匀强磁场。一束比荷（电荷量与质量之比）均为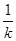
的带正电颗粒，以不同的速率沿着磁场区域的水平中心线O’O进入两金属板之间，其中速率为v0的颗粒刚好从Q点处离开磁场，然后做匀速直线运动到达收集板。重力加速度为g，PQ=3d，NQ=2d，收集板与NQ的距离为l，不计颗粒间相互作用。求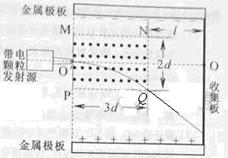
（1）电场强度E的大小；
（2）磁感应强度B的大小；
（3）速率为λv0(λ>1)的颗粒打在收集板上的位置到O点的距离。
2、选择题 带电粒子进入云室会使云室中的气体电离，从而显示其运动轨迹，图是在有匀强磁场的云室中观察到的粒子的轨迹，a和b是轨迹上的两点，匀强磁场B垂直纸面向里．该粒子在运动时，其质量和电荷量不变，而动能逐渐减少．下列说法正确的是（ ）
A．粒子先经过a点，再经过b点
B．粒子先经过b点，再经过a点
C．粒子带负电
D．粒子带正电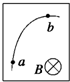
3、选择题 带电粒子在匀强磁场中运动，由于受到阻力作用，粒子的动能逐渐减小（带电荷量不变，重力忽略不计），轨道如曲线abc所示.则该粒子? (?)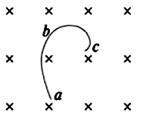
A．带负电，运动方向c→b→a
B．带负电，运动方向a→b→c
C．带正电，运动方向a→b→c
D．带正电，运动方向c→b→a
4、选择题 质子（m、e）和α粒子(4m、2e)以相同的速度垂直进入同一匀强磁场中，它们在垂直于磁场的平面内都做匀速圆周运动，它们的轨道半径和运动周期关系是：
A．Rp：Rα=1:2，Tp：Tα=1:2
B．Rp：Rα=2:1，Tp：Tα=1:2
C．Rp：Rα=1:2，Tp：Tα=2:1
D．Rp：Rα=1:4，Tp：Tα=1：4
5、计算题 如图所示，空间存在垂直XOY平面向里的匀强磁场，MN为一荧光屏，上下两面均可发光，当带电粒子打到屏上某点时，即可使该点发光，荧光屏位置如图，坐标为M（0，4.0），N（4.0，4.0）单位为cm。坐标原点O有一粒子源，可以发射沿XOY平面各个方向的电子（不计电子的重力），已知电子质量m=9.0×10-31kg，电量为e=1.6×10-19C，磁感应强度B=9.0×10-3T，求：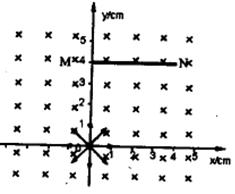
（1）若一电子以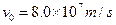
沿y轴正方向射入，求荧光屏上亮点坐标。
（2）若所有电子以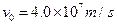
射入，求能打到M点的电子的速度入射方向。（用与X轴正方向的夹角或夹角的三角函数值表示）
（3）若所有电子以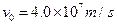射入，求荧光屏发光区域的坐标（坐标的单位为 cm）