时间:2019-07-02 23:32:58
1、选择题 (19分)如图甲所示,虚线MN上方存在垂直纸面向里的匀强磁场,MN下方存在竖直向下的匀强磁场,两处磁场磁感应强度大小相等。相距L=1.5 m的足够长的金属导轨竖直放置,导轨电阻不计。质量为m1=1kg的金属棒ab和质量为m2=0.27kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上,金属棒的电阻Rab=Rcd=0.9Ω,ab棒光滑,cd棒与导轨间动摩擦因数为μ=0.75。现由静止释放cd棒,同时ab棒受方向竖直向上,大小按图乙所示变化的外力F作用而运动,经研究证明ab棒做初速度为零的匀加速运动,g取10m/s2。
(1)求磁感应强度B的大小和ab棒加速度的大小;
(2)已知在前2s内外力F做功为40J,求这一过程中两金属棒产生的总焦耳热;
(3)求cd棒达到最大速度所需的时间t0。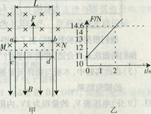
参考答案:(1) B=1.2T,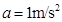
(2)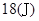 ;
;
(3)2s
本题解析:和ab棒加速度的大小;由动能定理及其相关知识列方程解出两金属棒产生的总焦耳热;运用摩擦定律、安培力、闭合电路欧姆定律、速度公式等列方程求出cd棒达到最大速度所需的时间t0。
解:(1)(7分)经过时间t,金属棒ab的速率: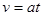 (1分)
(1分)
此时,回路中的感应电流: 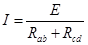 ?(1分)
?(1分)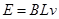 ?(1分)
?(1分)
对金属棒ab,由牛顿第二定律得: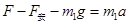 ?(1分)
?(1分)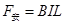 (1分)
(1分)
由以上各式整理得: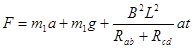
在图线上取两点:t1=0,F1=11N;
t2=2s,F2=14.6N
代入上式得: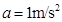 ?(1分)
?(1分)
B=1.2T?(1分)?
(2)(6分)在2s末金属棒ab的速率: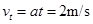 ?(1分)
?(1分)
所发生的位移: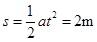 ?(1分)
?(1分)
由动能定理得: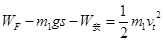 ?(2分)?
?(2分)?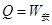 (1分)
(1分)
联立解得: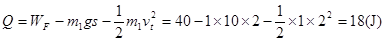 ?(1分)
?(1分)
(3)(6分)cd棒先做加速度逐渐减小的加速运动,当cd棒所受重力与滑动摩擦力相等时,速度达到最大,此时有: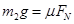 ?(1分)
?(1分)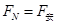 ?(1分)
?(1分)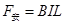 ?(1分)
?(1分)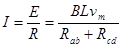 ?(1分)
?(1分)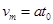 ?(1分)
?(1分)
整理得: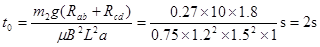 (1分)
(1分)
本题难度:一般
2、选择题 如图所示,为速度选择器原理图,Dl和 D2是两个平行金属板,分别连在电源的两极上,其间有一定的电场强度为E,同时在这空间加有垂直于电场方向的磁场,磁感应强度为B。Sl、S2为两个小孔,且Sl与S2连线方向与金属板平行。速度沿Sl、S2连线方向从Sl飞入的带电粒子只有做直线运动才可以从S2飞出,若让一束不同粒子沿Sl与S2连线方向从Sl孔飞入,则下列说法正确的是( )
A.能够从S2孔飞出的粒子必为同种粒子
B.能够从S2孔飞出的粒子必具有相同的速度
C.能够从S2孔飞出的粒子若改为从S2孔飞入,也必能从S1孔飞出
D.只有从S2孔飞出的带正电的粒子,若改为从S2孔飞入,才能从S1孔飞出
参考答案:B
本题解析:
试题分析:速度选择器是根据粒子通过复合场后,电场力与洛伦兹力平衡,则有被选择的速度v的大小应满足v="E/B" ,与粒子的正负无关,但必须从S1孔飞入,故A错误;B正确;能够从S2孔飞出的粒子若改为从S2孔飞入,不论粒子的正电荷,还是负电荷,电场力与洛仑兹力方向均相同,因此不能从S1孔飞出,故C、D错误;
考点: 带电粒子在复合场中运动
本题难度:一般
3、计算题 (18分)如图所示,圆心为原点、半径为R的圆将xOy平面分为两个区域,即圆内区域Ⅰ和圆外区域Ⅱ。区域Ⅰ内有方向垂直于xOy平面的匀强磁场B1。平行于x轴的荧光屏垂直于xOy平面,放置在坐标y=-2.2R的位置。一束质量为m、电荷量为q、动能为E0的带正电粒子从坐标为(-R,0)的A点沿x正方向射入区域Ⅰ,当区域Ⅱ内无磁场时,粒子全部打在荧光屏上坐标为(0,-2.2R)的M点,且此时,若将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变。若在区域Ⅱ内加上方向垂直于xOy平面的匀强磁场B2,上述粒子仍从A点沿x轴正方向射入区域Ⅰ,则粒子全部打在荧光屏上坐标为(0.4R,-2.2R)的 N点。求:
(1)打在M点和N点的粒子运动速度v1、v2的大小。
(2)在区域Ⅰ和Ⅱ中磁感应强度B1、B2的大小和方向。
(3)若将区域Ⅱ中的磁场撤去,换成平行于x轴的匀强电场,仍从A点沿x轴正方向射入区域Ⅰ的粒子恰好也打在荧光屏上的N点,则电场的场强为多大?
参考答案:(1) (2)
(2)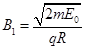 ,方向垂直xOy平面向外;
,方向垂直xOy平面向外; ,方向垂直xOy平面向里?(3)
,方向垂直xOy平面向里?(3)
本题解析:(1)粒子在磁场中运动时洛伦兹力不做功,打在M点和N点的粒子动能均为 ,速度
,速度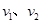 大小相等,设为
大小相等,设为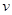 ,由
,由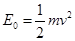 可得
可得 ?(2分)
?(2分)
(2)如图所示,区域Ⅱ中无磁场时,将荧光屏沿y轴负方向平移,粒子打在荧光屏上的位置不变,说明粒子速度垂直荧光屏向下,所以粒子在区域Ⅰ中运动四分之一圆周后,从C点沿y轴负方向打在M点,轨迹圆心是O1点,半径为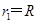 ?(2分)
?(2分)
区域Ⅱ有磁场时,粒子轨迹圆心是O2点,半径为r2,由几何关系得 ?(2分)
?(2分)
解得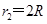 ?(1分)
?(1分)
由 得
得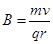 ?(1分)
?(1分)
故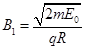 ,方向垂直xOy平面向外。?(2分)
,方向垂直xOy平面向外。?(2分) ,方向垂直xOy平面向里。?(2分)
,方向垂直xOy平面向里。?(2分)
(3)区域Ⅱ中换成匀强电场后,粒子从C点进入电场做类平抛运动,则有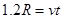 ,?(2分)
,?(2分) ?(2分)
?(2分)
解得场强 ?(2分)
?(2分)
本题难度:一般
4、简答题
⑴匀强电场的场强E;
⑵AD之间的水平距离d;
⑶已知小颗粒在轨迹DP上某处的最大速度为vm,该处轨迹的
曲率半径是距水平面高度的k倍,则该处的高度为多大?
参考答案:(1)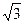 mg/q(2)
mg/q(2)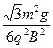 (3)
(3)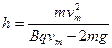
本题解析:⑴小球受力如图所示?qE=mgcotα…(2分)? E=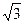 mg/q…………(2分)
mg/q…………(2分)
⑵设小球在D点速度为vD,在水平方向由牛顿第二定律得:
qE=max………………(1分)?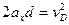 ………………………………(2分)
………………………………(2分)
小球在D点离开水平面的条件是:?qvDB=mg……………………………(1分)
得:d=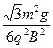 ……………………………………………………………(2分)
……………………………………………………………(2分) ⑶当速度方向与电场力和重力合力方向垂直
⑶当速度方向与电场力和重力合力方向垂直
时,速度最大,……………………(1分)
则: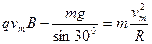 ……(2分)
……(2分)
R = kh ………………………………(1分)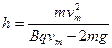 …………………(3分)
…………………(3分)
本题难度:一般
5、计算题 如图所示,以正方形abcd为边界的区域内有平行x轴指向+x方向的匀强电场和垂直纸面向星的匀强磁场,正方形的边长为L,带电粒子(不计重力)从Oc边的中点D,以某一初速度沿y轴正方向射入场区,恰好做直线运动。如果撤去磁场,保留电场,粒子仍以上述初速度从D点射入场区,则粒子从bc边的P点射出场区,设P点的坐标为(L,yp)。求:如果撤去电场,保留磁场,粒子仍以 上述的初速度从D点射入场区,在yP取不同值的情况下,粒子出射点在场区边界上的分布范围。
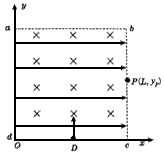
参考答案:解:设电场强度为E,磁感应强度为B,粒子电量为q,质量为m,初速度为v
当电场和磁场同时存在时,有:qBv=qE ①
撤去磁场,粒子在电场中的偏转距离为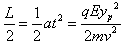 ②
②
撤去电场,设粒子在磁场中做圆周运动的半径为R。由洛伦兹力提供向心力,有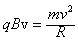 ③
③
在磁场中的偏转距离为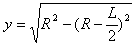 ④
④
由①②③④可得: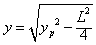 ⑤
⑤
由⑤可知,当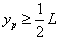 时,y≥0,即粒子从纵轴上射出 ⑥
时,y≥0,即粒子从纵轴上射出 ⑥
当yp=L时,由⑤得: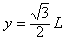 ⑦
⑦
所以,当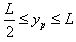 时,x=0,粒子出射点在纵轴上分布范围是:
时,x=0,粒子出射点在纵轴上分布范围是: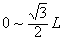 ⑧
⑧
当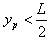 时,纵坐标y=0,出射点在横坐标上的分布范围是:
时,纵坐标y=0,出射点在横坐标上的分布范围是: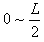 ⑨
⑨
本题解析:
本题难度:困难