时间:2019-06-29 06:02:55
1、计算题 为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是面积A=0.04m2的金属板,间距L=0.05m,当连接到U=2500V的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示。现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒1013个,假设这些颗粒都处于静止状态,每个颗粒带电量为q=+1.0×10-17 C,质量为m=2.0×10-15 kg,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力。求合上电键后:
(1)经过多长时间烟尘颗粒可以被全部吸附?
(2)除尘过程中电场对烟尘颗粒共做了多少功?
(3)经过多长时间容器中烟尘颗粒的总动能达到最大?

参考答案:解:(1)当最靠近上表面的烟尘颗粒被吸附到下板时,烟尘就被全部吸附,烟尘颗粒受到的电场力
F=qU/L
L=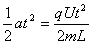
∴t=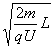 =0.02 (s)
=0.02 (s)
(2)W=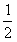 NALqU=2.5×10-4 (J)
NALqU=2.5×10-4 (J)
(3)设烟尘颗粒下落距离为x
Ek=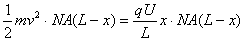
当x=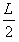 时,Ek达最大
时,Ek达最大
x=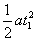
t1=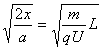 =0.014 (s)
=0.014 (s)
本题解析:
本题难度:困难
2、简答题 如图所示,在倾角37°的斜面两端,垂直于斜面方向固定两个弹性板,两板相距2米,质量10克,带电量1×10-7库仑的物体与斜面的摩擦系数为0.2,物体在斜面中点时速度大小为10米/秒,物体在运动中与弹性板碰撞中机械能不损失,物体在运动中电量不变,若匀强电场场强E=2×106牛/库,求物体在斜面上通过的路程?(g=10米/秒2)
参考答案:S=40m
本题解析: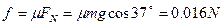 ,mgsin370=0.06N,Eq=0.2N,则f+ mgsin37°<Eq,故最后应停在紧靠上边弹性板处,由动能定理得:
,mgsin370=0.06N,Eq=0.2N,则f+ mgsin37°<Eq,故最后应停在紧靠上边弹性板处,由动能定理得:
本题难度:一般
3、计算题 如图所示,水平桌面处有水平向右的匀强电场,场强大小E=2´104V/m,A、B是完全相同的两个小物体,质量均为m=0.1kg,电量均为q=2´10-5C,且都带负电,原来都被按在桌面上的P点。现设法使A物体获得和电场E同方向的初速vA0=12m/s,A开始运动的加速度大小为6m/s2,经 时间后,设法使B物体获得和电场E同方向的初速vB0=6m/s(不计A、B两物体间的库仑力,运动过程中A,B的带电量不发生改变),求:
时间后,设法使B物体获得和电场E同方向的初速vB0=6m/s(不计A、B两物体间的库仑力,运动过程中A,B的带电量不发生改变),求: 
【小题1】小物体与桌面之间的阻力 为多大?
为多大?
【小题2】在A未与B相遇前,A电势能增量的最大值;
【小题3】如果要使A尽快与B相遇, 为多大?
为多大?
参考答案:
【小题1】0.2N
【小题2】4.8J
【小题3】4s
本题解析:(1)(3分)A释放后:qE+f=ma
得f=ma-qE= 0.2N
(2)(4分)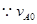 >
> ,且
,且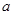 相同
相同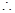 只能在A往返过程中与B相遇
只能在A往返过程中与B相遇
A速度减到零,经过的位移为s=vA02/2a=12m,tA=vA0/a=2s
DEmax=qEs=2×105×2×104×12 J=4.8J
(3)(5分)要使A在最短时间内与B相遇,则对应B减速到零时与A相遇。
B的最大位移:sB=vB02/2a=3m 运动时间:tB=vB0/a=1s
A返回时: qE-f=ma’ 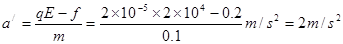
A返回走了s’=s-sB=9m 用时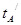 ==3s
==3s 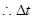 =tA+
=tA+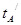 -tB=4s
-tB=4s
本题难度:一般
4、简答题 右下图为示波器的部分构造示意图,真空室中阴极K不断发出初速度可忽略的电子,电子经电压为U0的电场加速后,由孔N沿长为I、相距为d的两平行金属板A、B间的中心轴线进入两板间,电子穿过A、B后最终可打在中心为O的荧光屏CD上。若在AB间加上变化规律为 的交变电压,恰好能让t=0时刻进入AB间的电子经A板右边缘射出打在荧光屏上。假设在电子通过两板的极短时间内AB间电场可视为恒定不变。已知电子电荷量为e,质量为m,电子所受重力不计。求:
的交变电压,恰好能让t=0时刻进入AB间的电子经A板右边缘射出打在荧光屏上。假设在电子通过两板的极短时间内AB间电场可视为恒定不变。已知电子电荷量为e,质量为m,电子所受重力不计。求:
(1)电子通过孔N时的速度大小 ;
;
(2)A、B间电压的最大值Umax和有效值U。
参考答案:
(1)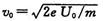 (2)
(2)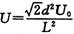
本题解析:
本题难度:一般
5、计算题 .(12分)如图所示,匀强电场方向沿x轴的正方向,场强为E.在A(l,0)点有一个质量为m,电荷?量为q的粒子,以沿y轴负方向的初速度v。开始运动,经过一段时间到达B(0,-l)点,(不计重力作用).求:
(1)粒子的初速度v0的大小;
(2)当粒子到达B点时的速度v的大小
参考答案:
本题解析:略
本题难度:一般