时间:2019-06-29 05:58:08
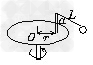
1、计算题 在水平转台上，距转轴为r处
插立一竖直杆
，杆顶系一根长为L的细绳，绳的末端挂一个质量为m的小球，如图所示，当转台匀速转动后，试证悬绳张开的角度α与转台转速n的关系是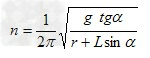
。
参考答案：证明：如图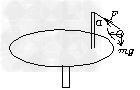
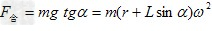? ①?
ω=2πn? ②
②代入①得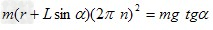
解得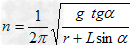
?
证毕。
本题解析：
本题难度：一般
2、选择题 如图所示，“旋转秋千”中的两个座椅A、B质量相等，通过相同长度的缆绳悬挂在旋转圆盘上．不考虑空气阻力的影响，当旋转圆盘绕竖直的中心轴匀速转动时，下列说法正确的是（ ）
A．A的速度比B的大
B．A与B的向心加速度大小相等
C．悬挂A、B的缆绳与竖直方向的夹角相等
D．悬挂A的缆绳所受的拉力比悬挂B的小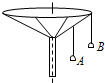
参考答案：AB两个座椅具有相同的角速度．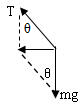
A：根据公式：v=ω?r，A的运动半径小，A的速度就小．故A错误；
B：根据公式：a=ω2r，A的运动半径小，A的向心加速度就小，故B错误；
C：如图，对任一座椅，受力如图，由绳子的拉力与重力的合力提供向心力，则得：mgtanθ=mω2r，则得tanθ=ω2rg，A的半径r较小，ω相等，可知A与竖直方向夹角θ较小，故C错误．
D：A的向心加速度就小，A的向心力就小，A对缆绳的拉力就小，故C错误；D正确．
故选：D
本题解析：
本题难度：简单
3、简答题 如图所示．地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动．地球的轨道半径为R，运转周期为T．地球和太阳中心的连线与地球和行星的连线所夹的角叫地球对该行星的观察视角（简称视角）．已知该行星的最大视角为θ，当?行星处于最大视角处时，是地球上的天文爱好者观察该行星的最佳时期．若某时刻该行星正处于最佳观察期，问该行星下一次处于最佳观察期至少需经历多长时间？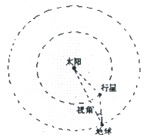
参考答案：由题意可得行星的轨道半径r=Rsinθ
设行星绕太阳的转动周期为T′由开普勒第三定律有：
R3T2=r3T′2
设行星最初处于最佳观察时期前，其位置超前于地球，且经时间t地球转过α角后，该行星再次处于最佳观察期，
则行星转过的较大为β=π+α+2θ
于是有：2πTt=α
2πT′t=β
解得：t=(π+2θ)
本题解析：
本题难度：一般
4、填空题 杂技演员表演“水流星”的方法如下：一根细绳的一端系有盛满水的小水桶，手拉绳的另一端，并以此为圆心，让小水桶在竖直平面内做圆周运动，如图所示，质量为0.5kg的小水桶里盛有1kg的水，表演时转动半径为1m，当水桶过最高点速度为4m/s时，水对桶底的压力大小为______；当水桶过最高点水恰好不溢出，则此时细绳拉力大小为______．（g=10m/s2．）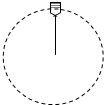
参考答案：对桶中的水分析有：mg+N=mv2r，代入数据得，N=6N，根据牛顿第三定律知，水对桶底的压力大小为6N．
? 当水桶过最高点时水恰好不溢出，则桶底对水的压力为0，有mg=mv02r．则v0=
本题解析：
本题难度：一般
5、选择题 游乐场中有一种叫“空中飞椅”的设施，其基本装置是将绳子上端固定在转盘的边缘上，绳子下端连接座椅，人坐在座椅上随转盘旋转而在空中飞旋，若将人和座椅看成质点，简化为如图所示的模型，其中P为处于水平面内的转盘，可绕竖直转轴OO′转动，已知绳长为l，质点的质量为m，转盘静止时悬绳与转轴间的距离为d．让转盘由静止逐渐加速转动，经过一段时间后质点与转盘一起做匀逮圆周运动，此时绳与竖直方向的夹角为θ，不计空气阻力及绳重，绳子不可伸长，则质点从静止到做匀速圆周运动的过程中，绳子对质点做的功为（ ）
A．
| 1 2 |
| 1 2 |
| 1 2 |
| 1 2 |
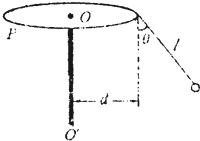
参考答案：设质点与转盘一起做匀速圆周运动时速度大小为v，由重力和绳子的拉力的合力提供质点圆周运动的向心力，如图，则
有
? mgtanθ=mv2d+lsinθ? ①
对于质点从静止到做匀速圆周运动的过程中，重力做功为-mgl（1-cosθ），设绳子拉力做功为W，则根据动能定理得：
?W-mgl（1-cosθ）=12mv2②
联立①②得：W=mgl（1-cosθ）+12mg(d+lsinθ)tanθ
故选A
本题解析：
本题难度：简单