时间:2019-06-29 05:37:19
1、计算题 一辆汽车沿平直公路以v0=10m/s匀速运动,忽然以加速度为2m/s2刹车,求汽车刹车后6s内的位移是多大?
参考答案:25m
本题解析:
本题难度:一般
2、选择题 一小滑块m从静止开始沿光滑斜面由A滑到C,经历的时间为t1;如果改由光滑曲面ADC滑到C,则经历的时间为t2.已知斜面越陡物体下滑的加速度越大,两个过程到达C点速度大小相等.则t1与t2的大小关系正确的是( )
A.t1>t2
B.t1=t2
C.t1<t2
D.已知条件不足,不能判定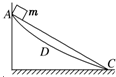
参考答案:A
本题解析:
本题难度:一般
3、简答题 为了减少战斗机起飞时在甲板上加速的时间和距离,现代航母大多采用了蒸汽弹射技术.一架总质量M=5.0x103kg的战机如果采用滑行加速(只依靠自身动力系统加速),要达到vo=60m/s的起飞速度,甲板水平跑道的长度至少为120m.采用蒸汽弹射技术,战机在自身动力和持续的蒸汽动力共同作用下只要水平加速60m就能达到起飞速度.假设战机起飞过程是匀加速直线运动,航母保持静止,空气阻力大小不变,取g=l0m/s2.
(1)采用蒸汽弹射技术,求战机加速过程中加速度大小以及质量m=60kg的飞行员受到座椅作用力的大小.
(2)采用蒸汽弹射技术,弹射系统的弹力为多大?弹力在加速60m的过程中对战机做的功是多少?
参考答案:(1)设战机在自身动力和蒸汽动力共同作用下滑行的加速度为a,
则由 V02=2as
解得 a=30m/s2 ,
飞行员受到座椅水平方向的作用力?Fx=ma=1.8×103 N,
飞行员受到座椅竖直方向的作用力 ?Fy=mg=6.0×102 N,
飞行员受到座椅作用力大小为 F=
本题解析:
本题难度:一般
4、简答题 高速公路上甲乙两车在同一车道上同向行驶,甲车在前,乙车在后,速度均为v0=30m/s,距离s0=100m,t=0时刻甲车遇紧急情况后,甲乙两车的加速度随时间变化如图所示,取运动方向为正方向.通过计算说明两车在0~9s内会不会相撞?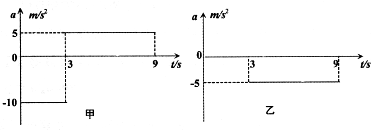
参考答案:由图象知,甲在前3s内的加速度a甲1=-10m/s2,在3-9s内的加速度a甲2=5m/s2,乙在前3s的加速度a乙1=0,在3-9s内的加速度a乙2=-5m/s2
根据图象分析知:甲前3s内做a甲1=-10m/s2匀减速直线运动,3s后速度减为0后再以a甲2=5m/s2做匀加速直线运动,乙在做匀速直线运动,3s后以a乙2=-5m/s2做匀减速直线运动.
甲车在匀减速过程中的初速度为30m/s,加速度为a甲1=-10m/s2可知3s后甲的速度刚好为0,故位移
x甲1=v+v02t=0+302×3m=45m
乙在前3s内的位移x乙1=vt=30×3m=90m
此时甲乙相距△x=x甲1+s0-x乙1=45+100-90m=55m
从此刻开始,甲做初速度为0加速度为a甲2=5m/s2的匀加速运动,乙做初速度为v0乙=30m/s,加速度a乙2=-5m/s2的匀减速直线运动,此时两车相距△x=55m
因为甲做匀加速运动,乙做匀减速运动,根据运动规律,在甲速度增加到和乙相等时两车末能相撞,则以后就不会相撞:
v甲=a甲2t ①
v乙=v乙0+a乙2t ②
当v甲=v乙时,可得运动时间t=3s
在这一过程中,甲的位移x甲2=12a甲2t2=12×5×32m=22.5m
乙的位移x乙2=v0乙t+12a乙2t2=30×3+12×(-5)×32m=67.5m
因为:x甲2+△x>x乙2
所以两车不会相撞.
答:两车在0-9s时间内不会相撞.
本题解析:
本题难度:一般
5、简答题 如图所示,倾角θ=37°的斜面固定在水平面上.质量m=0.5kg的小物块受到沿斜面向上的F=9.0N的拉力作用,从斜面底端由静止沿斜面向上运动.小物块与斜面间的动摩擦因数μ=0.25(斜面足够长,取g=10m/s2.sin37°=0.6,cos37°=0.8).
(1)求在拉力F的作用过程中,小物块加速度的大小;
(2)若在小物块沿斜面向上运动x1=0.80m时,将拉力F撤去,求整个运动过程中小物块重力势能的最大值.(取水平面做参考平面)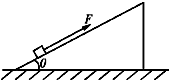
参考答案:(1)根据牛顿第二定律,有:F-f-mgsin37°=ma1?
而f=μmgcos37°?
故所求加速度为a1=10m/s2
(2)设撤去拉力时小物块的速度为v,撤去拉力后小物块加速度和向上运动的距离大小分别为a2、x2,有
a2=gsinθ+μgcosθ=8m/s2?
对加速过程,有v2=2a1x1
对减速过程,有v2=2a2x2
解得x2=1.0m?
所求重力势能的最大值为Epm=mg(x1+x2)sin37°=5.4J
答:(1)求在拉力F的作用过程中,小物块加速度的大小10m/s2;
(2)若在小物块沿斜面向上运动x1=0.80m时,将拉力F撤去,求整个运动过程中小物块重力势能的最大值为5.4J.
本题解析:
本题难度:一般