时间:2019-06-29 05:14:31
1、计算题 如图所示,一个质量为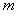 、电荷量为
、电荷量为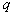 的正离子,在
的正离子,在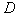 处沿图示方向以一定的速度射入磁感应强度为
处沿图示方向以一定的速度射入磁感应强度为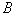 的匀强磁场中,此磁场方向是垂直纸面向里。结果离子正好从距
的匀强磁场中,此磁场方向是垂直纸面向里。结果离子正好从距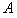 点为
点为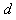 的小孔
的小孔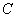 沿垂直于电场方向进入匀强电场,此电场方向与
沿垂直于电场方向进入匀强电场,此电场方向与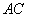 平行且向上,最后离子打在
平行且向上,最后离子打在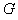 处,而
处,而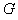 处距
处距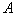 点
点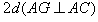 。不计离子重力,离子运动轨迹在纸面内。求:
。不计离子重力,离子运动轨迹在纸面内。求:
(1)正离子从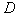 处运动到
处运动到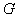 处所需时间为多少?
处所需时间为多少?
(2)正离子到达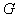 处时的动能为多少?
处时的动能为多少? 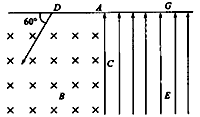
2、计算题 (14分)如图所示,图中左边有一对平行金属板,两板相距为d,电压为U。两板之间有匀强磁场,磁感应强度大小为B0,方向与金属板面平行并垂直于纸面朝里;图中右边有一半径为R、圆心为O的圆形区域,区域内也存在匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。一电荷量为q的正离子沿平行于金属板面、垂直于磁场的方向射入平行金属板之间,沿同一方向射出平行金属板之间的区域,并沿直径PQ方向射入磁场区域,最后从圆形区域边界上的G点射出,已知弧QG所对应的圆心角为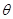 。离子重力不计。求:
。离子重力不计。求: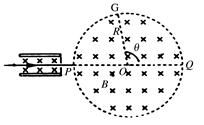
(1)离子速度的大小;
(2)离子在圆形磁场区域内做圆周运动的半径;
(3)离子的质量。
3、选择题 .如图所示为一速度选择器,两极板P、Q之间距离为d,且P接电源负极,Q接正极;板内有一磁感应强度为B,方向垂直纸面向外的匀强磁场,一束粒子流以速度v流经磁场时恰好不偏转(不计重力),则两极板必须加上一定电压U;则下列说法中正确的是(?)
A.U=Bvd,粒子一定带正电
B.U=Bv,粒子一定带负电
C.U=Bvd,粒子一定从a运动到b
D.U=Bvd,粒子可能从b运动到a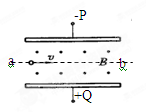
4、计算题 一带正电的粒子带电量为q,质量为m。从静止开始经一电压U1=100V的匀强电场加速后,垂直进入一电压U2=40V的平行板电场,平行板长L=0.2m,间距d=1cm。在平行板区域同时存在一垂直纸面向里的匀强磁场,磁感应强度B1=1T。粒子穿过平行板后进入另一垂直向里的有界匀强磁场区域,磁感应强度为B2,宽度D=0.1m。最后从此磁场的右边界以
60°穿出(如图所示)。已知粒子的比荷为 ,忽略粒子重力及阻力的影响。
,忽略粒子重力及阻力的影响。
(1)求粒子进入平行板电场时的速度大小;
(2)求有界匀强磁场的磁感应强度B2的大小;
(3)求粒子从进入磁场到穿出磁场所用时间。(保留一位有效数字)
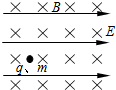
5、选择题 如图所示,水平向右的匀强电场场强为E,垂直纸面向里的水平匀强磁场磁感应强度为B,一带电量为q的液滴质量为m,在重力、电场力和洛伦兹力作用下做直线运动,下列关于带电液滴的性质和运动的说法中正确的是( )
A.液滴可能带负电
B.液滴一定做匀速直线运动
C.不论液滴带正电或负电,运动轨迹为同一条直线
D.液滴不可能在垂直电场的方向上运动