时间:2019-06-29 05:07:19
1、填空题 如图甲是利用激光测转速的原理示意图，图中圆盘可绕固定轴转动，盘边缘侧面上有一小段涂有很薄的反光材料，当盘转到某一位置时，接收器可以接收到反光涂层所反射的激光束，并将所收到的光信号立即转变成电信号，在示波器显示屏上显示出来。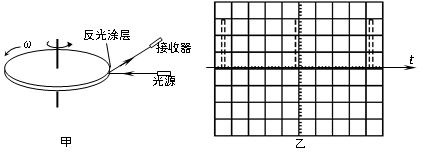
(1)若图乙中示波器显示屏上横向的每小格对应的时间为1.00×10-2s（即乙图中t轴每大格表示5.00×10-2s），则圆盘的转速为________r/s。(保留3位有效数字)
(2)若测得圆盘直径为11cm，则可求得圆盘侧面反光涂层的长度为________cm。(保留3位有效数字)
参考答案：（1）(1) 4.55? (3分)? (2)1.57cm? (3分)
本题解析：
试题分项：（1）由乙图可知，圆盘转动的周期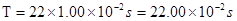
?，根据转速、角速度和周期的关系
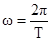和
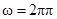，得到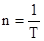
，代入数据， 
。
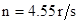（2）由乙图可知，反光涂层经过接收器的时间
，根据弧长和线速度的关系，得
；再由
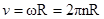，则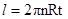
，代入数据，得到
。
本题难度：一般
2、选择题 质量为m的小球在竖直平面内的圆形轨道的内侧运动，经过最高点而不脱离轨道的临界速度值是v，当小球以2v的速度经过最高点时，对轨道的压力值为( )
A．mg
B．2mg
C．3mg
D．4mg
参考答案：C
本题解析：当小球以速度v经内轨道最高点时，小球仅受重力，重力充当向心力，有
；
当小球以速度2v经内轨道最高点时，小球受重力G和向下的支持力N，如图，
合力充当向心力，有
；又由牛顿第二定律得到，小球对轨道的压力与轨道对小球的支持力相等，N′=N；由以上三式得到，N′=3mg；故答案选C；
考点：向心力；牛顿第二定律；牛顿第三定律．
点评：本题要注意对小球受力分析，找出向心力来源；同时，题中要求的为轨道对小球的压力，而非支持力！
本题难度：一般
3、选择题 如图所示，A、Ｂ两质点绕同一圆心按顺时针方向做匀速圆周运动，Ａ的周期为Ｔ１，Ｂ的周期为Ｔ２，且Ｔ１
参考答案：
本题解析：
本题难度：一般
4、选择题 【改编】有关圆周运动的基本模型，下列说法正确的是（ ）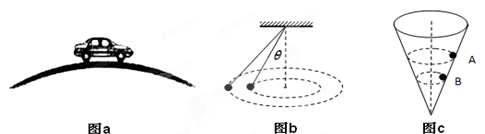
A．如图a，汽车通过拱桥的最高点时的速度越大，汽车对拱桥的压力就越大
B．如图b所示是一圆锥摆，减小θ，但保持圆锥的高不变，则θ越小，圆锥摆的周期越小
C．如图c，同一小球在光滑而固定的圆锥筒内的A、B位置先后分别做匀速度圆周运动，则在A、B两位置小球的角速度及所受筒壁的支持力大小相等
D．火车转弯时的速度小于规定速度行驶时，内轨对内轮缘会有挤压作用
参考答案：D
本题解析：汽车通过拱桥的最高点时有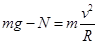
，故得
，所以速度越大，受支持力越小，汽车对桥的压力也越小，A错误；圆锥摆过程中重力和绳子的拉力充当向心力，故有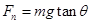
，设圆锥的高度为h，则运动半径为
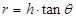，故有
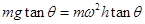，解得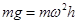
，角速度大小与角度无关，再
，所以周期与角度无关，所以B错误；在两个位置上小球的重力相同，支持力方向相同，所以合力相同，即向心力相同，根据公式
可得半径越大，角速度越小，故角速度不同，所受筒壁的支持力大小相等，故C错误；当火车在规定的速度转弯时，由支持力与重力的合力提供火车转弯所需的向心力．当速度小于规定的速度时，火车的支持力与重力的合力大于火车转弯需要的向心力，导致火车轮缘挤压内轨，故D正确。
考点：圆周运动
本题难度：一般
5、计算题 如图所示，ABDO是处于竖直平面内的固定光滑轨道，AB是半径为R=15m的
圆周轨道，半径OA处于水平位置，BDO是半径为 r =7.5m的半圆轨道，D为BDO轨道的中点。一个小球P从A点的正上方距水平半径OA高H处自由下落，沿竖直平面内的轨道通过D点时对轨道的压力等于重力的
倍。g取10m/s2。求：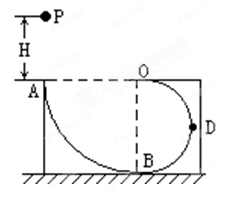
小题1: H的大小。
小题2:说明此球能否达到BDO轨道的O点，
小题3:小球沿轨道运动后再次落到轨道上的速度大小是多少？
参考答案：
小题1:10m
小题2:能
小题3: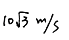
本题解析：：（1）设小球通过D点的速度为v，则有：m
=F=
mg
小球从P点落下直到沿光滑轨道运动的过程中，机械能守恒，有mg（H+
）=
mv2
可得高度H=
R=10m
（2）设小球能够沿竖直半圆轨道运动到O点的最小速度为vc，有m
=mg
小球至少应从Hc高处落下，mgHC=mvC2?解得HC=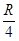
由H＞HC，小球可以通过O点．
（3）小球由H落下通过O点的速度为v0=
=14.1m/s
小球通过O点后作平抛运动，设小球经时间t落到AB圆弧轨道上，有x=v0t? y=gt2
且x2+y2=R2?可解得时间t="1s" （另解舍弃）落到轨道上速度的大小v=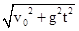
=17.3m/s
本题难度：简单