时间:2019-06-29 04:59:07
1、选择题 A、B两条船静止在水面上,它们的质量均为M。质量为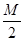 的人以对地速度v从A船跳上B船,再从B船跳回A船,经过几次后人停在B船上。不计水的阻力,则(?)
的人以对地速度v从A船跳上B船,再从B船跳回A船,经过几次后人停在B船上。不计水的阻力,则(?)
A、A、B两船速度均为零? B、vA:vB=3:2
C、vA:vB=2:1?D、vA:vB=2:3
参考答案:B
本题解析:人和船开始都处于静止状态,动量为零,在水平方向上因不计水的阻力,故人和船水平方向动量守恒,人最后停在B船上,满足 ,解得
,解得 ,故只有B选项正确。
,故只有B选项正确。
本题难度:一般
2、简答题 (1)2011年3月,日本地震引发海啸,继而福岛核电站(世界最大的核电站)发生核泄漏.关于核电站和核辐射,下列说法中正确的是______.
A.核反应堆发生的是轻核聚变反应
B.核反应堆发生的是重核裂变反应
C.放射性同位素的半衰期长短由核内部本身决定,与外部条件无关
D.放射性同位素的半衰期长短与地震、风力等外部环境有关
(2)如图所示,A、B两木块靠在一起放于光滑的水平面上,A、B的质量分别为mA=2.0kg和mB=1.5kg.一个质量为mC=0.5kg的小铁块C以v0=4m/s的速度滑到木块A上,离开木块A后最终与木块B一起匀速运动.木块A在铁块C滑离后的速度为vA=0.4/m/s.求:
①铁块C在滑离A时的速度;
②最终木块B的速度.
参考答案:
(1)核电站是利用重核的裂变来发电的,重核的裂变形成的链式反应是可在人工控制下进行的.而轻核的聚变现在是无法人工控制的,核反应堆发生的是重核裂变反应,所以选项B正确、A错误.
放射性元素衰变的快慢是由核内部自身的因素决定的,跟原子所处的化学状态和外部条件没有关系.所以选项C正确、D错误.
故答案为:BC
(2)①铁块C在滑离A的瞬间,由动量守恒得,mcvo=(mA+mB)vA+mcvc?
代入数据解得vc=1.2m/s
②铁块C和木块B相互作用最终和B达到相同的速度
铁块C和木块A、B作用过程中动量守恒,
mcvo=mAvA+(mC+mB)vB?
代入数据解得vB=0.6m/s
答:铁块C在滑离A时的速度为1.2m/s,最终木块B的速度为0.6m/s
本题解析:
本题难度:一般
3、计算题 如图所示,在光滑水平面上的甲、乙两车质量分别为1kg、4kg,甲车以10m/s的速度向右运动与静止的乙车发生碰撞,碰后乙车获得3m/s的速度。求甲车碰后的速度。
参考答案:甲的速度大小为2m/s,方向与甲的初速度方向相反。
本题解析:设甲车的初速度方向为正方向
m甲v0=m甲v甲’+m乙v乙’
v甲’= v0- m乙v乙’/m甲
v甲’=-2m/s
故甲的速度大小为2m/s,方向与甲的初速度方向相反。
本题难度:简单
4、实验题 如图所示装置通过半径相同的A、B两球(质量分别为mA、mB)的碰撞来验证动量守恒定律。实验时先使A球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹。重复上述操作10次,得到10个落点痕迹。再把B球放在水平槽上靠近槽末端的地方,让A球仍从位置G由静止开始滚下,和B球碰撞后,A、B球分别在记录纸上留下各自的落点痕迹。重复这种操作10次,得到如图所示的三个落点。用刻度尺分别测量三个落点的平均位置离O点的距离,即线段OM、OP、ON的长度。 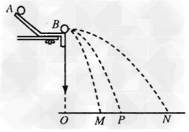
(1)两小球的质量关系应为mA___________mB(选填“大于”“小于”或“等于”);
(2)碰撞过程中动量守恒,则由图可以判断出N是_____球的落点,P是_____球的落点;
(3)用题中的字母写出动量守恒定律的表达式__________。
参考答案:(1)大于?
(2)B,A?
(3)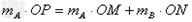
本题解析:
本题难度:一般
5、计算题 (10分)如图所示,质量为3m的木块静止放置在光滑水平面上,质量为m的子弹(可视为质点)以初速度v0水平向右射入木块,穿出木块时速度变为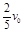 ,试求:
,试求: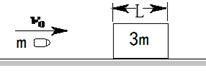
①子弹穿出木块后,木块的速度大小;
②子弹穿透木块的过程中产生的热量。
参考答案:①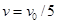 ;②
;②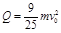
本题解析:①设子弹穿出木块后,木块的速度大小为v,以向右方向为正方向,根据动量守恒定律有: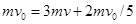 解得
解得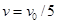
②设子弹穿透木块的过程中,产生的热量为Q,由能量守恒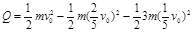 ?解得
?解得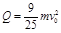
本题难度:一般