时间:2019-06-28 05:46:48
1、计算题 如图所示,A,B为两个大小可视为质点的小球,A的质量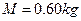 ,B的质量
,B的质量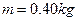 ,B球用长
,B球用长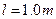 的轻质细绳吊起,当细绳位于竖直位置,B球处于静止状态时,B球恰好与弧形轨道MN的末端接触但无作用力,已知弧形轨道的内表面光滑,且末端切线水平,现使A球从距轨道末端
的轻质细绳吊起,当细绳位于竖直位置,B球处于静止状态时,B球恰好与弧形轨道MN的末端接触但无作用力,已知弧形轨道的内表面光滑,且末端切线水平,现使A球从距轨道末端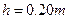 的高处由静止释放,当A球运动到轨道末端时与B球发生完全弹性碰撞。若
的高处由静止释放,当A球运动到轨道末端时与B球发生完全弹性碰撞。若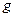 取
取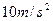 ,求:
,求:
小题1:A球刚要接触到B球时的速度大小;
小题2:两小球相碰撞过程中,B球对A球所做的功;
小题3:两个小球碰撞后各自开始运动的瞬间,B球对细绳的拉力大小。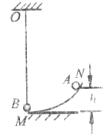
参考答案:
小题1: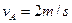
小题2:-1.15J
小题3:
本题解析:(1)
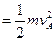
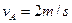
(2)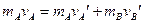
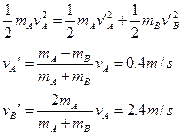
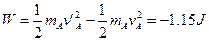
(3)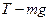


本题难度:一般
2、选择题 用一根细绳,一端系住一定质量的小球,小球大小忽略.另一端固定在天花板上,使小球做如图的匀速圆周运动.现在有如图5两个这样的装置(a)和(b),(a)、(b)图中,两球转动的角速度大小相同,绳与竖直方向的夹角分别为37°和53°.则a、b两球的转动半径Ra和Rb之比,以及相对应的绳子的长度La和Lb之比分别为:(sin37°=0.6;cos37°=0.8)( )
A.Ra:Rb=9:16;La:Lb=4:3
B.Ra:Rb=9:16;La:Lb=3:4
C.Ra:Rb=3:4;La:Lb=9:16
D.Ra:Rb=3:4;La:Lb=16:9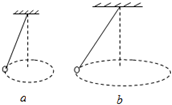
参考答案:小球所受的合力F合=mgtanθ=mrω2,则角速度的大小ω=
本题解析:
本题难度:一般
3、简答题 图甲所示为一根竖直悬挂的不可伸长的细绳,下端拴一小物块A,上端固定在C点且与一能测量绳的拉力传感器相连.已知有一质量为m0的子弹B沿水平方向以速度v0射入A内(未穿透),接着两者一起绕C点在竖直平面内做圆周运动,在各种阻力都忽略的条件下测力传感器测得绳的拉力
F随时间t的变化关系如图乙所示.已知子弹射入的时间极短,且图乙中
t=0为A、B开始以相同速度运动的时刻,根据力学规律和题中(包括图)提供的信息,试求A的质量?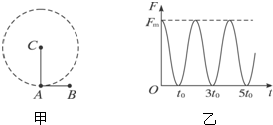
参考答案:在最低点有:Fm-(m0+mA)g=(m0+mA)v2l? ①
在最高点,绳子拉力为零,有(m0+mA)g=(m0+mA)v′2l? ②
从最高点到最低点,根据动能定律得,(m0+mA)g?2l=12(m0+mA)v2-12(m0+mA)v′2? ③
子弹射入A内的过程动量守恒,根据动量守恒定律得,m0v0=(m0+mA)v? ④
联立①②③④解得mA=Fm6g-m0
故A的质量为Fm6g-m0
本题解析:
本题难度:一般
4、选择题 如图所示,质量分别为m1、m2的小球A 、B 可以在光滑的水平杆上滑动,两球之间用一根水平细线相连,m1=2m2.当装置以角速度ω绕中心轴线匀速转动,达到平衡时,两球离轴的距离保持不变,则有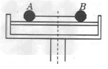
[? ]
A. 两球的向心力大小相等
B. 
C.两球的向心加速度大小相等
D.当ω增大时,B球向外运动
参考答案:BD
本题解析:
本题难度:一般
5、简答题 如图所示,将一质量为m=0.1kg的小球自水平平台右端O点以初速度v0水平抛出,小球飞离平台后由A点沿切线落入竖直光滑圆轨道ABC,并沿轨道恰好通过最高点C,圆轨道ABC的形状为半径R=2.5m的圆截去了左上角l27°的圆弧,BC为其竖直直径,(sin53°=0.8?cos53°=0.6,重力加速度g取10m/s2)求: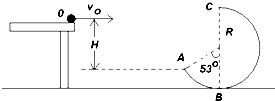
(1)小球经过C点的速度大小;
(2)小球运动到轨道最低点B?时小球对轨道的压力大小;
(3)v0的数值.
参考答案:(1)恰好运动到C点,有重力提供向心力,即
mg=mvC2R
解得:vc=5m/s?
(2)从B点到C点,由机械能守恒定律有
12mvc2+2mgR=12mvB2
在B点对小球进行受力分析,由牛顿第二定律有
FN-mg=mvB2R
解得:FN=6N
根据牛顿第三定律,小球对轨道的压力大小为6.0N
(3)从A到B由机械能守恒定律有
12mvA2+mgR(1-cos53°)=12mvB2
解得:
vA=
本题解析:
本题难度:一般