时间:2019-06-28 04:30:17
1、简答题 大气中存在可自由运动的带电粒子,其密度随距地面高度的增加而增大,可以把离地面50km以下的大气看作是具有一定程度漏电的均匀绝缘体(即电阻率较大的物质);离地面50km以上的大气则看作是带电粒子密度非常大的良导体。地球本身带负电,其周围空间存在电场,离地面L=50km处与地面之间的电势差约为U=3.0×105V。由于电场的作用,地球处于放电状态,但大气中频繁发生雷暴又对地球充电,从而保证了地球周围电场恒定不变。统计表明,雷暴每秒带给地球的平均电荷量为q=1800C。试估算大气电阻率ρ和地球漏电功率P。(已知地球半径r=6400km,结果保留一位有效数字)
参考答案:ρ=2×1012Ω·m-1?P=UI=5×108W
本题解析:已知每秒雷暴带给地球的电荷量为q,则大气的漏电电流为I=q/t=1800A
大气的漏电电阻可由欧姆定律求得U=IR其中U=3.0×105V,R=ρL/s,L=50km,s=4πr2,代入有关数据解得,ρ=2×1012Ω·m-1?地球的漏电功率为P=UI=5×108W
本题难度:简单
2、选择题 要使一个电压表的量程变大,可采用的方法是(? )
A.并联一个阻值较大的电阻
B.把原有的分压电阻换成阻值较大的电阻
C.再串联一个阻值适当的分压电阻
D.在原有的分压电阻上并联一个适当的电阻
参考答案:BC
本题解析:使一个电压表的量程变大,即在通相同电流时,该部分能承担较大电压,所以可以串联一个阻值适当的分压电阻,C对。电压表本身是由表头串联分压电阻改装得到的,要扩大量程,也可以把原有的分压电阻换成阻值较大的电阻,B对。
本题难度:简单
3、选择题 有一个带电量为+q,重为G的小球,从两竖直的带电平行板上方h处自由落下,两极板间匀强磁场的磁感应强度为B,方向如图所示,则带电小球通过有电场和磁场的空间时( )
A.有可能做匀速运动
B.有可能做匀加速直线运动
C.不可能做曲线运动
D.一定做曲线运动
参考答案:若小球进入磁场时电场力和洛伦兹力相等,由于小球向下运动时,速度会增加,小球所受的洛伦兹力增大,将不会再与小球所受的电场力平衡,不可能做匀加速直线运动,也不可能做匀速直线运动.
若小球进入磁场时电场力和洛伦兹力不等,则合力方向与速度方向不在同一条直线上,小球做曲线运动.
综上所述,小球一定做曲线运动.故D正确,A、B、C错误.
故选D.
本题解析:
本题难度:一般
4、计算题 如图所示,真空中有以O′为圆心,r为半径的圆形匀强磁场区域,磁场方向垂直纸面向外,磁感应强度为B。圆的最下端与x轴相切于直角坐标原点O,圆的右端与平行于y轴的虚线MN相切,在虚线MN右侧x轴上方足够大的范围内有方向竖直向下、场强大小为E的匀强电场,在坐标系第四象限存在方向垂直纸面向里、磁感应强度大小也为B的匀强磁场,现从坐标原点O沿y轴正方向发射速率相同的质子,质子在磁场中做半径为r的匀速圆周运动,然后进入电场到达x轴上的C点。已知质子带电量为+q,质量为m,不计质子的重力、质子对电磁场的影响及质子间的相互作用力。求:
(1)质子刚进入电场时的速度方向和大小;
(2)OC间的距离;
(3)若质子到达C点后经过第四限的磁场后恰好被放在x轴上D点处(图上未画出)的一检测装置俘获,此后质子将不能再返回电场,则CD间的距离为多少。
参考答案:(1)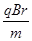 ?方向沿x轴正方向?(2)r+
?方向沿x轴正方向?(2)r+ ?(3)
?(3)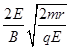
本题解析:(1)质子在磁场中做匀速圆周运动,洛伦兹力提供向心力,
根据牛顿第二定律得qvB=
解得?
质子运动轨迹如下图,
因为圆形匀强磁场区域的半径为r,质子在磁场中做匀速圆周运动的半径也为r,所以四边形 是菱形,由几何知识知,质子刚进入电场时的速度方向沿x轴正方向.
是菱形,由几何知识知,质子刚进入电场时的速度方向沿x轴正方向.
(2)质子沿y轴正方向射入磁场,则以N为圆心转过 圆弧后从A点垂直电场方向进入电场,进入电场后质子做类平抛运动,设质子电场中运动时间t , 则在y方向上有
圆弧后从A点垂直电场方向进入电场,进入电场后质子做类平抛运动,设质子电场中运动时间t , 则在y方向上有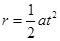
由牛顿第二定律得? qE=ma
解得 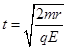
在x方向上,由题意可知x1=ON=r
电场中x2=NC=v
所以OC间的距离为x=x1+ x2 =r+
(3)设质子出电场时在竖直方向的速度为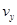 ,质子合速度为
,质子合速度为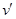 ,则
,则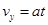
质子合速度与x轴正向夹角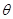 的正弦值为sinθ=
的正弦值为sinθ=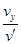
质子到达C点后进入第四限的磁场的运动轨迹如下图所示,设质子在第四限磁场中运动的轨道半径为R.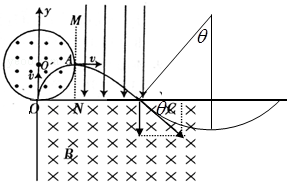
根据圆的性质,由几何知识得:
x3="CD=" 2R sinθ
质子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律得qvB= ,
,
运动半径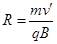
以上各式联立解得:x3="CD=" 2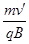
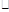
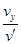 =
=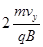 =
=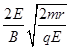
本题难度:一般
5、简答题 如图所示,在直角坐标系的I、Ⅱ象限内有垂直于纸面向里的匀强磁场,第Ⅲ象限有沿y轴负方向的匀强电场,第Ⅳ象限内无电场和磁场。质量为m,电荷量为q的粒子由M点以速度 沿x轴负方向进入电场,不计粒子的重力,粒子经N和x轴上的P点最后又回到M点。设OM=OP =l,ON=2l,求:
沿x轴负方向进入电场,不计粒子的重力,粒子经N和x轴上的P点最后又回到M点。设OM=OP =l,ON=2l,求:
(1)电场强度E的大小;
(2)匀强磁场磁感应强度B的大小;
(3)粒子从M点进入电场,经N、P点最后又回到M点所用的时间t。
参考答案:见解析
本题解析:(1)根据粒子在电场中的运动情况可知,粒子带负电,粒子在电场中运动所用的时间设为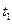
在x方向有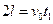 ?①
?①
在y方向有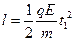 ?②
?②
解得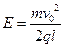 ?③
?③
(2)设粒子到达N点的速度为v,运动方向与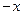 轴夹角
轴夹角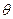
由动能定理得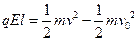 ?④
?④
将③式代入,得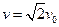
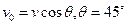
粒子在磁场中做匀速圆周运动,经过P点时的速度方向也与负x方向成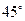 ,从P到M做直线运动,NP=NO+OP=3l
,从P到M做直线运动,NP=NO+OP=3l
粒子在匀强磁场中在洛伦兹力的作用下做匀速圆周运动,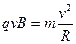
半径为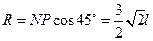
联立上述各式解得
(3)粒子在电场中运动所用时间为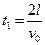
粒子在磁场中所用时间为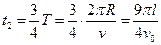
由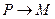 匀速直线运动所用时间
匀速直线运动所用时间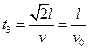
粒子从M进入电场,经N、P点最后又回到M点所用的时间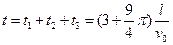 .
.
本题难度:一般