时间:2019-06-28 04:30:17
1、计算题 如图1所示，宽度为d的竖直狭长区域内（边界为L1、L2），存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场（如图2所示）。电场强度的大小为E0，E>0表示电场方向竖直向上t=0时，一带正电、质量为m的微粒从左边界上的N，点以水平速度v射入该区域，沿直线运动到Q点后，做一次完整的圆周运动，再沿直线运动到右边界上的N2点。Q为线段N1N2的中点，重力加速度为g。上述d、E0、m、v、g为已知量。
（1）求微粒所带电荷量q和磁感应强度B的大小；
（2）求电场变化的周期T；
（3）改变宽度d，使微粒仍能按上述运动过程通过相应宽度的区域，求T的最小值。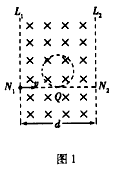 
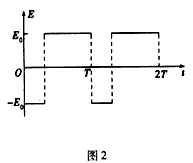
参考答案：解：（1）微粒做直线运动，则mg +qE0= qvB ①
微粒做圆周运动，则mg=qE0②
联立①②得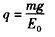
③
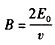④
（2）设微粒从N1运动到Q的时间为t1，做圆周运动的周期为t2，则2πR=vt1⑦
联立③④⑤⑥⑦得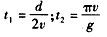
⑧
电场变化的周期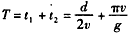
⑨
（3）若微粒能完成题述的运动过程，要求d≥2R ⑩
联立③④⑥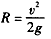
设N1Q段直线运动的最短时间为t1min，
由⑤⑩得
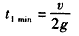
因t2不变，T的最小值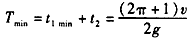
。
本题解析：
本题难度：困难
2、计算题 在如图甲所示的平面直角坐标系xOy中，存在沿x方向按如图乙所示规律周期性变化的匀强电场，沿x轴正方向为正。沿垂直于xOy平面指向纸里的方向存在按如图丙所示规律周期性变化的匀强磁场。在图甲中坐标原点O处有带正电的粒子，从t＝0时刻无初速度释放。已知粒子的质量m＝5×10－10kg，电荷量q＝1×10－6C，不计粒子的重力。求：
（1）t＝0.25×10－3s时粒子的速度及位置；
（2）t＝1×10－3s时粒子的位置坐标；
（3）t＝8×10－3s时粒子的速度。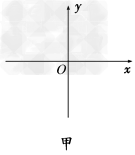
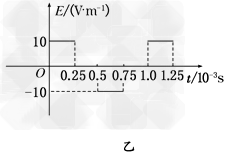
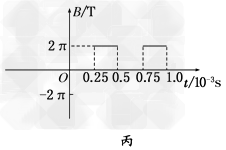
参考答案：解：（1）在第一个t0＝0.25×10－3s内粒子的加速度a满足：qE＝ma
末速度v1＝at0＝5m/s
沿x轴正向运动L1＝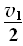
t0＝6.25×10－4m
(2)在0.25×10－3～0.5×10－3s内粒子做匀速圆周运动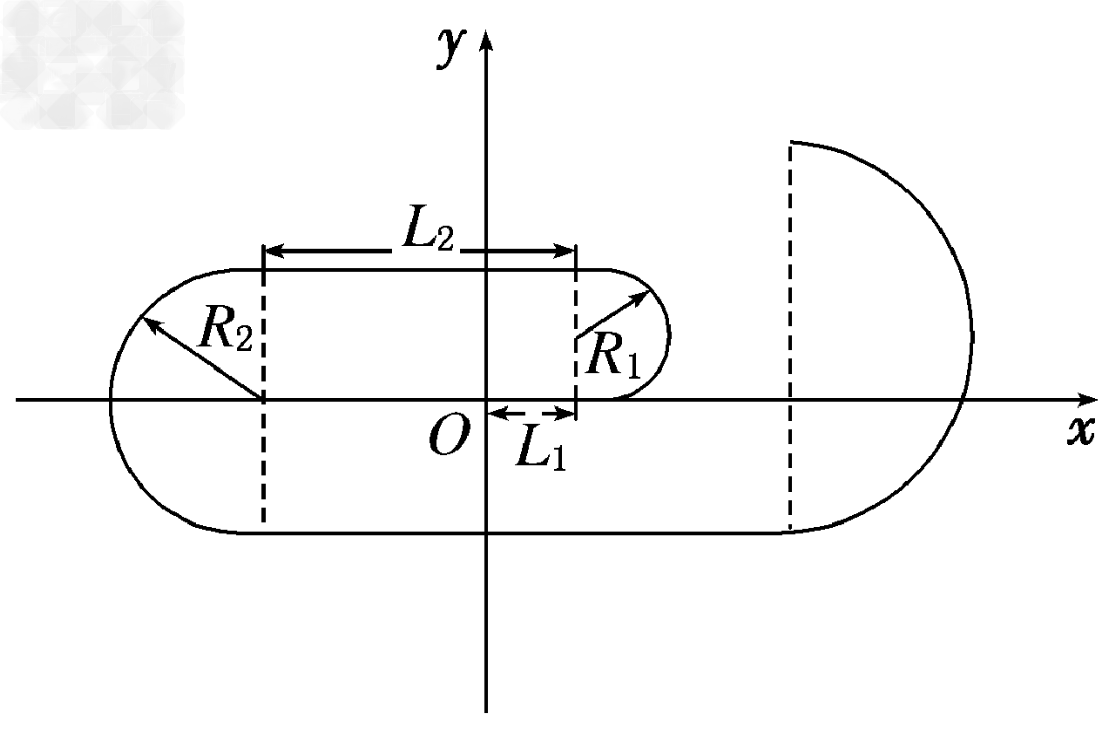
T＝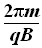
＝0.5 ×10－3s
故粒子在0.25×10－3s这段时间内运动了半个圆周
圆周运动的半径R1＝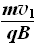
在0.5×10－3～0.75×10－3s内粒子沿x轴负向匀加速运动
末速度大小v2＝v1＋at0＝2v1
位移大小L2＝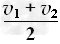
t0＝3L1
在0.75×10－3～1×10－3s内粒子做匀速圆周运动
R2＝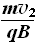
＝2R1
末位置坐标：x＝－(L2－L1)＝－1.25×10－3m
y＝－(2R2－2R1)＝－8 ×10－4m。
(3)粒子在8×10－3s内16次加速，每次速度增加v1，故：v＝16v1，v＝80m/s
方向沿x轴正向
本题解析：
本题难度：困难
3、选择题 如图所示，在空间中存在匀强电场和匀强磁场，磁场方向垂直纸面向里，电场方向平行于水平地面向右．一带电粒子在空间中从N沿着虚线运动到M，带电粒子的重力不可忽略，则以下说法正确的是（ ）
A．带电粒子一定带正电
B．带电粒子可能带正电
C．粒子将做匀速运动，则其动能、电势能均保持不变
D．粒子的电势能减小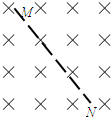
参考答案：
A、根据做直线运动的条件和受力情况（如图所示）可知，微粒一定带负电，且做匀速直线运动，所以选项A错误．
B、根据做直线运动的条件和受力情况（如图所示）可知，微粒一定带负电，且做匀速直线运动，所以选项B错误．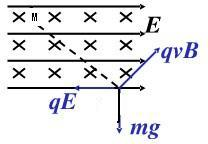
C、由能量守恒可知，电势能减小，机械能一定增加，所以选项C错误；
D、由于电场力向左，对微粒做正功，电势能一定减小，选项D正确．
故选D．
本题解析：
本题难度：一般
4、选择题 如图所示，质量为m、电荷量为q的带电液滴从h高处自由下落，进入一个互相垂直的匀强电场和匀强磁场区域，磁场方向垂直纸面，磁感应强度为B，电场强度为E。已知液滴在此区域中做匀速圆周运动，则圆周运动的半径R为（?）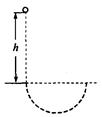
A．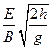
B．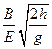
C．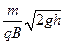
D．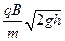
参考答案：AC
本题解析：∵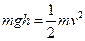
，
?∴
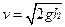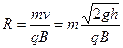
又∵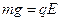
，∴
。
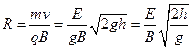本题难度：一般
5、选择题 在如图所示的匀强电场和匀强磁场共存的区域内，电子（不计重力）可能沿水平方向向右作直线运动的是（ ）
A．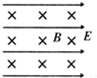
B．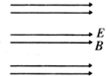
C．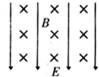
D．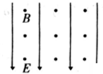
?
参考答案：A、若电子向右运动，则受到电场力向左，洛伦兹力向下，合力跟初速度方向不在同一直线上，故A错误；
B、若电子向右运动，则受到电场力向左，不受洛伦兹力，合力跟初速度方向在同一直线上，故B正确；
C、若电子向右运动，则受到电场力向上，洛伦兹力向下，当电场力等于洛伦兹力时，电子向右匀速运动，故C正确；
D、若电子向右运动，则受到电场力向上，洛伦兹力向上，合力跟初速度方向不在同一直线上，故D错误；
故选BC．
本题解析：
本题难度：一般