时间:2019-06-26 04:56:05
1、选择题 如图两个内壁光滑、半径不同的半球形碗，放在不同高度的水平面上，使两碗口处于同一水平面．现将质量相同的两个小球（小球半径远小于碗的半径），分别从两个碗的边缘由静止释放（忽略空气阻力），则
 |
参考答案：BC
本题解析：据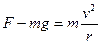
，
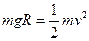可知C正确，两小球机械能守恒，故B正确. 【命题主旨】考查力学问题综合应用.
本题难度：一般
2、选择题 如图所示，物体A静止在光滑的水平面上，A的左边固定有轻质弹簧，与A质量相等的物体B以速度v向A运动并与弹簧发生碰撞，A、B始终沿同一直线运动，则A、B组成的系统动能损失最大的时刻是（ ）
A．开始运动时 B．A的速度等于v时
C．弹簧压缩至最短时 D．B的速度最小时
参考答案：C
本题解析：试题分析：A、B和弹簧看作糸统只有弹簧弹力做功，所有糸统机械能守恒。
，所以当
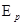最达时，A、B组成的糸统动能最小。
考点：机械能守恒定律
本题难度：一般
3、计算题 （10分）（创编）如图所示，质量为m、电量为-q的小球，可在半径为R的固定半圆形光滑的绝缘轨道两端点M，N之间来回滚动，磁场磁感强度B垂直于轨道平面，小球在M、N处速度为零。若小球在最低点的最小压力为零，那么磁感强度B为多大？小球对轨道最低点的最大压力为多大？
（已知重力加速度为g）
参考答案：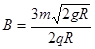
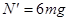
本题解析：
洛伦兹力不改变速度的大小，小球向左和向右通过轨道的最低点速度大小是一样的，但洛伦兹力的方向相反。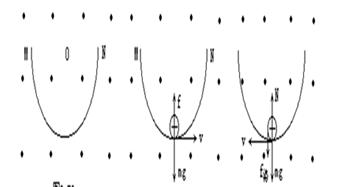
小球由M处静止滑下，到最低点的速度为v，由动能定理（或机械能守恒定律）
①
在最低点处，由向心力公式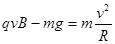 
②
联立①②式得：。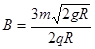
小球从N点静止滑下，到最低点对轨道压力最大，由动能定理（或机械能守恒定律） ③
④
由③、④式解得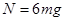 
。 由牛顿第三定律。
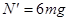考点：带电粒子在匀强磁场中的运动；圆周运动；向心力。
本题难度：一般
4、计算题 如图所示，一个截面为直角三角形的劈形物块固定在水平地面上．斜面,高h=4m，a=37°,一小球以Vo=9m/s的初速度由C点冲上斜面．由A点飞出落在AB面上．不计一切阻力．（Sin37°=0．6,cos37° =0．8,g="10" m/s2）求．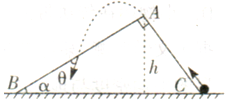
（l）小球到达A点的速度大小；
（2）小球由A点飞出至第一次落到AB面所用时间；
（3）小球第一次落到AB面时速度与AB面的夹角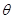
的正切值
参考答案：（1）1m/s（2）0.25s （3）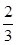
本题解析：(1)从C到A对小球运用动能定理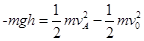
解得v0=1m/s
(2)将小球由A点飞出至落到AB面的运动分解为沿斜面（x轴）和垂直于斜面（y轴）两个方向;则落回斜面的时间等于垂直于斜面方向的时间
所以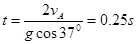
（3）小球落回斜面时沿斜面方向速度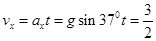
垂直斜面方向速度vy=1m/s
所以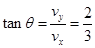
考点：动能定理及斜抛运动.
本题难度：一般
5、计算题 如图所示，AB是一个固定在竖直面内的弧形轨道，与竖直圆形轨道BCD在最低点B平滑连接，且B点的切线是水平的；BCD圆轨道的另一端D与水平直轨道DE平滑连接。B、D两点在同一水平面上，且B、D两点间沿垂直圆轨道平面方向错开了一段很小的距离，可使运动物体从圆轨道转移到水平直轨道上。现有一无动力小车从弧形轨道某一高度处由静止释放，滑至B点进入竖直圆轨道，沿圆轨道做完整的圆运动后转移到水平直轨道DE上，并从E点水平飞出，落到一个面积足够大的软垫上。已知圆形轨道的半径R=0.40m，小车质量m=2.5kg，软垫的上表面到E点的竖直距离h=1.25m、软垫左边缘F点到E点的水平距离s=1.0m。不计一切摩擦和空气阻力，弧形轨道AB、圆形轨道BCD和水平直轨道DE可视为在同一竖直平面内，小车可视为质点，取重力加速度g =10m/s2。
（1）要使小车能在竖直圆形轨道BCD内做完整的圆周运动，则小车通过竖直圆轨道最高点时的速度至少多大；
（2）若小车恰能在竖直圆形轨道BCD内做完整的圆周运动，则小车运动到B点时轨道对它的支持力多大；
（3）通过计算说明要使小车完成上述运动，其在弧形轨道的释放点到B点的竖直距离应满足什么条件。
参考答案：（1）2.0m/s（2）FN=150N（3）H≥1.0m
本题解析：（1）设小车能在竖直圆形轨道BCD内做完整的圆周运动，小车通过圆轨道最高点时的最小速度为vC，
根据牛顿第二定律有 mg=m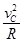
1分
解得vC=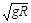
=
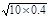m/s =2.0m/s 1分
（2）小车恰能在圆轨道内做完整的圆周运动，此情况下小车通过B点的速度为vB，轨道对小车的支持力为FN。
根据机械能守恒定律有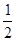 
mv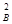
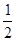=mvC2+2mgR 2分
根据牛顿第二定律有FN－mg=m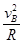
1分
解得 FN=150N 1分
（3）设小车从E点水平飞出落到软垫上的时间为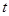
，则h=
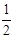gt2，
解得t=0.50s 1分
设小车以vE的速度从E点水平飞出落到软垫F点右侧，则vEt＞s，解得vE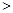
2.0m/s
要使小车完成题目中所述运动过程，应当满足两个条件：
①小车通过轨道B点的速度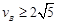
m/s；
②小车通过E点的速度vE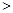2.0 m/s。
因vE= vB，综合以上两点，小车通过B点的速度应不小于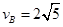
m/s 1分
设释放点到B点的竖直距离为H，根据机械能守恒定律有mgH=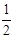 mvB2，解得H=1.0m
释放点到B点的竖直距离H≥1.0m 1分
考点：考查了牛顿第二定律，圆周运动，机械能守恒定律的应用
本题难度：一般