时间:2019-06-26 04:50:10
1、选择题 半径相等的两个小球甲和乙，在光滑的水平面上沿同一直线相向运动，若甲球质量大于乙球质量，发生碰撞前，两球的动能相等，则碰撞后两球的状态可能是?（填选项前的字母）
A．两球的速度方向均与原方向相反，但它们动能仍相等
B．两球的速度方向相同，而且它们动能仍相等
C．甲、乙两球的动量相同
D．甲球的动量不为零，乙球的动量为零
参考答案：C
本题解析： 根据动量与动能关系
可知
，根据动量守恒可各，碰撞后的总动量沿甲原来的方向，故甲继续沿原来的方向运动，乙被弹回，所以选项A错误；碰撞后，甲的动能减小，若为弹性碰撞，则乙的动能增大，故两者动能不相等；若为完全非弹性碰撞，碰撞后速度相等，动能不等 ，所以选项B错误；两球碰撞过程中动量守恒，碰撞后动量可能相等，所以选项C正确；因碰撞后，甲乙都沿甲原来的方向运动，故乙的动量不为零，所以选项D错误；
本题难度：一般
2、计算题 如图所示，一质量为M的平板车B放在光滑水平面上，在其右端放一质量为m的小木块A，m＜M，A、B间动摩擦因数为μ，现给A和B以大小相等、方向相反的初速度v0，使A开始向左运动，B开始向右运动，最后A不会滑离B，求：
（1）A、B最后的速度大小和方向；
（2）从地面上看，小木块向左运动到离出发点最远处时，平板车向右运动的位移大小。
参考答案：解：（1）由A、B系统动量守恒定律得：Mv0－mv0=（M+m）v
所以v=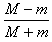
v0，方向向右
（2）A向左运动速度减为零时，到达最远处，此时板车移动位移为s，速度为v′，则由动量守恒定律得：Mv0－mv0=Mv′ ①
对板车应用动能定理得：-μmgs=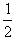
Mv′2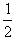－Mv02 ②
联立①②解得：s=
v02
本题解析：
本题难度：一般
3、简答题 质量相等且m1、m2都等于1kg的两个小球在光滑的水平面上分别以速度v1=2m/s、v2=1m/s同向运动并发生对心碰撞，碰后m2被右侧的墙原速弹回，又与m1相碰，碰后两球都静止．求两球第一次碰后m2球的速度大小．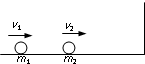
参考答案：两个球两次碰撞过程中，系统动量守恒，根据动量守恒定律得：
本题解析：
本题难度：一般
4、简答题 如图所示，光滑水平面上，质量为m的小球B连接着轻质弹簧，处于静止状态，质量为2m的小球A以大小为v0的初速度向右运动，接着逐渐压缩弹簧并使B运动，过一段时间，A与弹簧分离．
（1）当弹簧被压缩到最短时，弹簧的弹性势能Ep多大？
（2）若开始时在B球的右侧，某位置固定一挡板，在A球与弹簧未分离前使B球与挡板碰撞，并在碰后立刻将挡板撤走，设B球与挡板的碰撞时间极短，碰后B球的速度大小不变但方向相反，欲使此后弹簧被压缩到最短时，弹性势能达到第（1）问中Ep的2.5倍，必须使B球的速度多大时与挡板发生碰撞？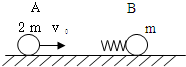
参考答案：（1）当弹簧压缩到最短时，A、B的速度相等，2mv0=3mv1 ①
A和B的共同速度v1=23v0
根据系统的机械能守恒得 12?2mv02=12?3mv12+Ep?②
解得 此时弹簧的弹性势能Ep=13mv02?③
（2）B碰挡板时没有机械能损失，碰后弹簧被压缩到最短时，A、B速度也相等，12?2mv02=12?3mv22+Ep′④
? Ep′=2.5Ep=56mv02
解得v2=±v03⑤
取向右为正方向．若v2=v03，则表示B球与板碰撞后，A、B此时一起向右运动．B球与板碰撞前B与A动量守恒
?2mv0=2?mvA+mvB⑥
B球与板碰撞后B与A动量也守恒
? 2mvA-mvB=3m?v03⑦
解得?vA=34v0，vB=v02
因为此时vA＞vB，弹簧还将继续缩短，所以这种状态是能够出现的，
若v2=-v03，则表示B球与板碰撞后A、B向左运动，B球与板碰撞后B和A动量守恒
? 2mvA-mvB=3mv2=-3m?v03?⑧
由⑥⑧可得，vA=v04，vB=32v0?
此时A、B球的总动能EK总=12?2mvA2+12mvB2=m（v04）2+12（32v0）2=1916mv02?
EK总大于A球最初的动能mv02，因此vB=32v0这种状态是不可能出现的，因此必须使B球在速度为v02时与挡板发生碰撞．?⑨
答：
（1）当弹簧被压缩到最短时，弹簧的弹性势能Ep为13mv02．
（2）必须使B球在速度为v02时与挡板发生碰撞．
本题解析：
本题难度：一般
5、简答题 如图所示，质量M=0.040kg的靶盒A静止在光滑水平导轨上的O点，水平轻质弹簧一端栓在固定挡板P上，另一端与靶盒A连接．Q处有一固定的发射器B，它可以瞄准靶盒发射一颗水平速度为v0=50m/s，质量m=0.010kg的弹丸，当弹丸打入靶盒A后，便留在盒内，碰撞时间极短．不计空气阻力．求：弹丸进入靶盒A后，弹簧的最大弹性势能为多少？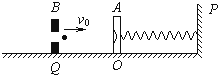
参考答案：（1）弹丸进入靶盒A后，弹丸与靶盒A的共同速度设为v，由系统动量守恒得：
mv0=（m+M）v
靶盒A的速度减为零时，弹簧的弹性势能最大，由系统机械能守恒得：
Ep=12（m+M）v2
解得：Ep=m22(m+M)v02
代入数值得Ep=2.5J
答：弹丸进入靶盒A后，弹簧的最大弹性势能为2.5J．
本题解析：
本题难度：一般