时间:2019-06-26 04:45:41
1、选择题 如图，带电平行金属板中匀强电场方向竖直上，匀强磁场方向垂直纸面向里，带电小球从光滑绝缘轨道上的a点由静止滑下，经过1/4圆弧轨道从端点P（切线水平）进入板间后恰好沿水平方向做直线运动，现使带电小球从比a点稍低的b点由静止滑下，在经过P点进入板间的运动过程中
[? ]
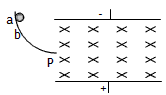
A．带电小球的动能将会增大
B．带电小球的电势能将会增大
C．带电小球所受洛伦兹力将会减小
D．带电小球所受电场力将会增大
参考答案：AB
本题解析：
本题难度：一般
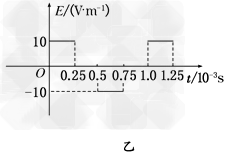
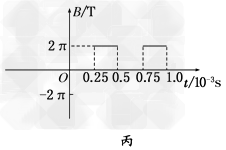
2、计算题 在如图甲所示的平面直角坐标系xOy中，存在沿x方向按如图乙所示规律周期性变化的匀强电场，沿x轴正方向为正。沿垂直于xOy平面指向纸里的方向存在按如图丙所示规律周期性变化的匀强磁场。在图甲中坐标原点O处有带正电的粒子，从t＝0时刻无初速度释放。已知粒子的质量m＝5×10－10kg，电荷量q＝1×10－6C，不计粒子的重力。求：
（1）t＝0.25×10－3s时粒子的速度及位置；
（2）t＝1×10－3s时粒子的位置坐标；
（3）t＝8×10－3s时粒子的速度。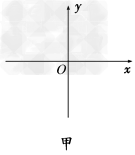
参考答案：解：（1）在第一个t0＝0.25×10－3s内粒子的加速度a满足：qE＝ma
末速度v1＝at0＝5m/s
沿x轴正向运动L1＝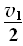
t0＝6.25×10－4m
(2)在0.25×10－3～0.5×10－3s内粒子做匀速圆周运动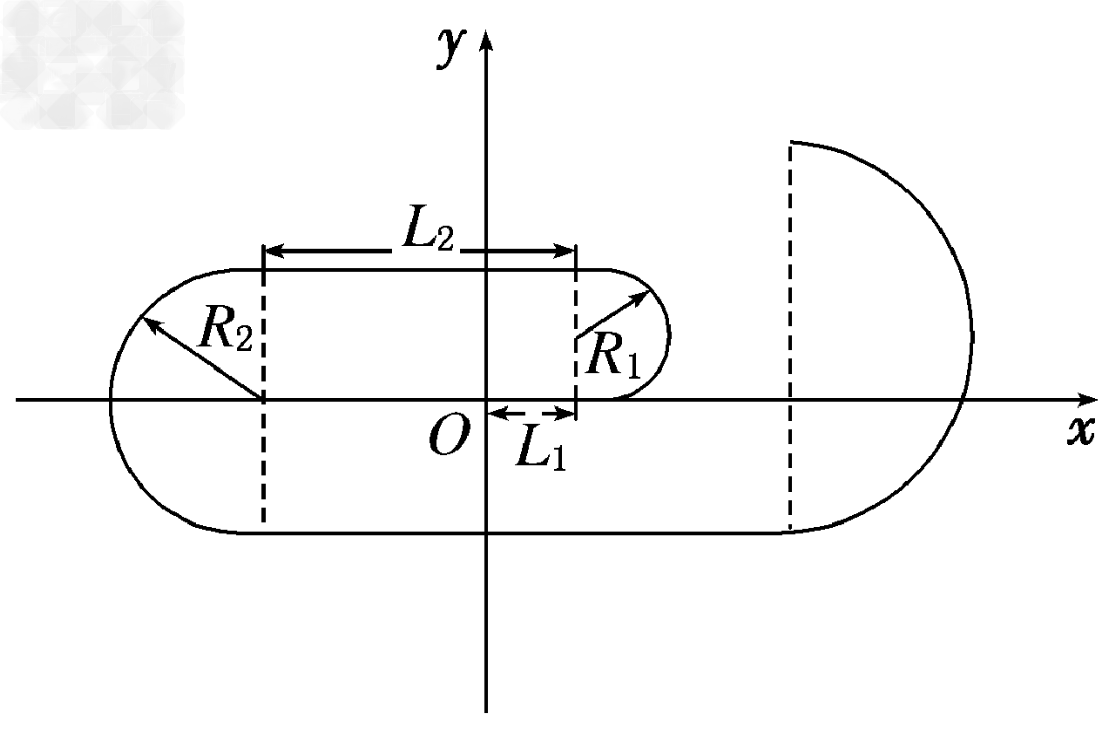
T＝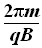
＝0.5 ×10－3s
故粒子在0.25×10－3s这段时间内运动了半个圆周
圆周运动的半径R1＝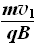
在0.5×10－3～0.75×10－3s内粒子沿x轴负向匀加速运动
末速度大小v2＝v1＋at0＝2v1
位移大小L2＝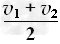
t0＝3L1
在0.75×10－3～1×10－3s内粒子做匀速圆周运动
R2＝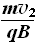
＝2R1
末位置坐标：x＝－(L2－L1)＝－1.25×10－3m
y＝－(2R2－2R1)＝－8 ×10－4m。
(3)粒子在8×10－3s内16次加速，每次速度增加v1，故：v＝16v1，v＝80m/s
方向沿x轴正向
本题解析：
本题难度：困难
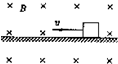
3、选择题 如图所示，质量为m电量为q的带正电物体，在磁感强度为B、方向直纸面向里的匀强磁场中，沿动摩檫因数为μ的水平面向左运动，则（ ）
A．物体的速度由v减小到零所用的时间等于
| mv μ(mg+qvB) |
| mv μ(mg+qvB) |
| μ(mg+qvB) q |
| (mg+qvB) q |
参考答案：A、B、对物体受力分析，受重力、支持力，洛伦兹力和滑动摩擦力；根据左手定则，洛伦兹力向下，合力向后，物体做减速运动；由于摩擦力f=μ（mg+qvtB），不断减小，加速度不断减小，不是匀变速运动，故物体的速度由v减小到零所用的时间大于mvμ(mg+qvB)，故A错误，B也错误；
C、若另加一个电场强度为μ(mg+qvB)q、方向水平向左的匀强电场，电场力F=qE=μ（mg+qvB）=f，物体受力平衡，做匀速直线运动，故C正确；
D、若另加一个电场强度为(mg+qvB)q、方向竖直向上的匀强电场，电场力F=qE=mg+qvB，支持力为零，故摩擦力为零，物体做匀速直线运动，故D正确；
故选CD．
本题解析：
本题难度：简单
4、选择题 如图所示，竖直放置足够长的平行光滑导轨间距d=lm、其电阻不计，磁感应强度B=1T、方向垂直纸面向里，匀质导体棒AB长L=2m、电阻r=1Ω、质量为m=0.lKg；电阻R1=R2=1Ω，现让棒AB由静止释放（与导轨接触良好）．下降到虚线位置时达到最大速度，下列说法正确的是（g= 10m/s2）
A．棒AB的最大速度为1m/s
B．通过R1的最大电流为lA
C．闭合回路的路端电压是0.5v
D．棒AB最大电功率为1W
参考答案：ACD
本题解析：导体棒速度最大时重力等于洛伦兹力，
,
，通过R1最大电流0.5A，闭合回路的路端电压
,棒AB最大功率
,所以选ACD。
本题难度：简单
5、计算题 如图所示，一条长为L的绝缘细线上端固定，下端拴一质量为m的带电小球，将它置于水平方向的匀强电场中，电场强度为E，已知当细线与竖直方向的夹角为α时，小球处于平衡位置A点，问在平衡位置给小球多大的速度vA，刚好能使之在电场中作竖直平面内的完整圆周运动？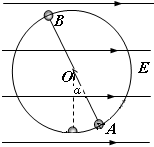
参考答案：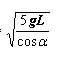
本题解析：
为临界条件，所以有：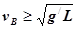
从A点到B点过程，仅重力、电场力对小球做功，由动能定理得：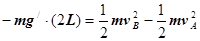
联立以上各式解得：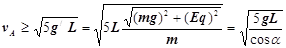
本题难度：一般