时间:2019-06-26 04:00:48
1、简答题 如图所示,小球沿水平面冲上一竖直面内光滑的半圆形轨道,轨道半径为R,小球在轨道的最高点对轨道压力等于小球的重力,问
(1)小球离开轨道最高点后落到地面时,小球的水平位移是多少?
(2)小球落地时速度大小是多少?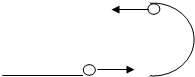
参考答案:(1)根据牛顿第二定律得:mg+mg=mv2R
解得:v=
本题解析:
本题难度:一般
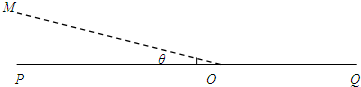
2、简答题 如图所示,在竖直平面内,虚线MO与水平线PQ相交于O,二者夹角θ=30°,在MO左侧存在电场强度为E、方向竖直向下的匀强电场,MO右侧某个区域存在磁感应强度为B、垂直纸面向里的匀强磁场,O点处在磁场的边界上,现有一群质量为m、电量为+q的带电粒子在纸面内以速度v(0≤v≤
| E B |
参考答案:
(1)粒子的运动轨迹如图所示,设粒子在匀强磁场中做匀速圆周运动的半径为R,周期为T,粒子在匀强磁场中运动时间为t1
则?qvB=mv2R
解得:R=mvqB?
T=2πmBq?
t1=13T?
设粒子自N点水平飞出磁场,出磁场后应做匀速运动至OM,设匀速运动的距离为s,匀速运动的时间为t2,由几何关系知:
s=Rtanθ?
t2=sv?
过MO后粒子做类平抛运动,设运动的时间为t3,
则:32R=12qEmt32?
又由题知:v=EB
则速度最大的粒子自O进入磁场至重回水平线POQ所用的时间为:
t=t1+t2+t3=2(3
本题解析:
本题难度:一般
3、实验题 (1)在做平抛实验的过程中,小球在竖直放置的坐标纸上留下三点痕迹,如图是小球做平抛运动的闪光照片,图中每个小方格的边长都是0.54cm,已知闪光频率是30Hz,那么重力加速度g=___________m/s2,小球的初速度是___________m/s,球过A点时的速率是___________m/s。(小数点后保留二位) 
(2)如图a是研究小球在斜面上平抛运动的实验装置,每次将小球从弧型轨道同一位置静止释放,并逐渐改变斜面与水平地面之间的夹角θ,获得不同的射程x,最后作出了如图b所示的x-tanθ图象,g=10m/s2。则:由图b可知,小球在斜面顶端水平抛出时的初速度v0=___________。实验中发现θ超过60°后,小球将不会掉落在斜面上,则斜面的长度为___________。 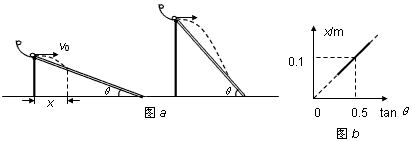
参考答案:(1)9.72,0.49,0.81?
(2)1m/s,
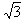 m
m
本题解析:
本题难度:一般
4、选择题 如图所示,在竖直放置的半圆形容器的中心O点分别以水平速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB相互垂直且OA与竖直方向成α角,求两小球初速度之比v1∶v2。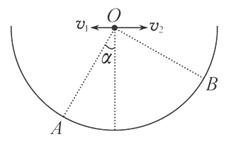
参考答案: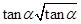
本题解析:两质点抛出后都做平抛运动,设容器的半径为R,两质点运动的时间分别为tA、tB
对A球:Rsinα=v1tA,
Rcosα=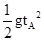
对B球:Rcosα=v2tB
Rsinα=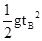
联立解得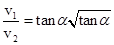
本题难度:一般
5、选择题 在冬奥会自由式滑雪比赛中,运动员在较高的雪坡上滑到某一弧形部位处,沿水平方向飞离斜坡,在空中划过一段抛物线后,再落到雪坡上,如图所示,若雪坡的倾角为θ,飞出时的速度大小为v0,则( )
A.运动员落回雪坡时的速度大小是
| v0 cosθ |
| 2v0tanθ g |
| 2v02sinθ gcos2θ |
| 2v02 g |
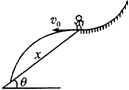
参考答案:设在空中飞行时间为t,运动员在竖直方向做自由落体运动,水平方向做匀速直线运动,则两方向位移关系:12gt2v0t=gt2v0=tanθ,则有飞行的时间t=2v0tanθg,所以B正确;
因此竖直方向的速度大小为:vy=gt=2v0tanθ,竖直方向的高度是h=12gt2=2v20tan2θg,所以D正确;
落回雪坡时的速度大小v=
本题解析:
本题难度:一般