时间:2019-06-26 03:55:12
1、计算题 (选修3-5选做题)
动量分别为5kgm/s和6kgm/s的小球A、B沿光滑平面上的同一条直线同向运动,A追上B并发生碰撞后。若已知碰撞后A的动量减小了2kgm/s,而方向不变,那么A、B质量之比的可能范围是什么?
参考答案:解:A能追上B,说明碰前vA>vB,则 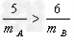
碰后A的速度不大于B的速度,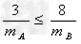
又因为碰撞过程系统动能不会增加,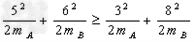
由以上不等式组解得: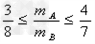
本题解析:
本题难度:一般
2、计算题 下面是一个物理演示实验,它显示:图中自由下落的物体A和B经反弹后,B能上升到比初始位置高得多的地方。A是某种材料做成的实心球,质量m1=0.28kg,在其顶部的凹坑中插着质量m2=0.10kg的木棍B。B只是松松地插在凹坑中,其下端与坑底之间有小空隙。将此装置从A下端离地板的高度H=1.25m处由静止释放。实验中,A触地后在极短时间内反弹,且其速度大小不变;接着木棍B脱离球A开始上升,而球A恰好停留在地板上。重力加速度g=10m/s2。求:
(1)实心球A与地面碰撞之前瞬间的速度;
(2)木棍B上升的高度。 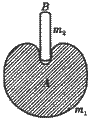
参考答案:解:根据题意,A碰地板后,反弹速度的大小v1等于它下落到地面时速度的大小,即
v1=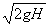
A刚反弹后,速度向上,立刻与下落的B碰撞,碰前B的速度?
v2=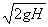
由题意,碰后A速度为零,以v2′表示B上升的速度,根据动量守恒,有?
m1v1-m2v2=m2v2′
令h表示B上升的高度,有
h=v2′2/2g
由以上各式并代入数据,得
h=4.05m
本题解析:
本题难度:一般
3、计算题 如果α粒子以速度v与电子发生弹性正碰(假定电子原来是静止的),求碰撞后仅粒子的速度变化了多少?并由此说明:为什么原子中的电子不能使α粒子发生明显的偏转?
参考答案:解:设α粒子初速度为v,质量为M,与电子碰后速度为v1,电子质量为m,与α粒子碰后速度为v2
由动量守恒定律得Mv=Mv1+mv2 ①
由能量关系得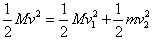 ?②
?②
由①②得碰后α粒子速度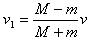 ③
③
α粒子速度变化量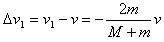 ④
④
把M=7 300m代入④得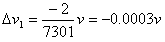
可见α粒子的速度变化只有万分之三,说明原子中的电子不能使α粒子发生明显的偏转
本题解析:
本题难度:一般
4、计算题 在核反应堆中,常用减速剂使快中子减速。假设减速剂的原子核质量是中子的k倍,中子与原子核的每次碰撞都可看成是弹性正碰,设每次碰撞前原子核可认为是静止的。求N次碰撞后中子速率与原速率之比。
参考答案:解:设中子和作减速剂的物质的原子核A的质量分别为 和
和 ,碰撞后速度分别为
,碰撞后速度分别为 和
和 ,碰撞前后的总动量和总能量守恒,有
,碰撞前后的总动量和总能量守恒,有
?  ?①
?①
?  ?②
?②
? 式中 为碰撞前中子速度,由题设
为碰撞前中子速度,由题设
?  ?③
?③
? 由①②③式得,经1次碰撞后中子速率与原速率之比为
?  ?④
?④
? 经N次碰撞后,中子速率与原速率之比为
?  ?⑤
?⑤
本题解析:
本题难度:困难
5、计算题 如图所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为m的小球从高为h处由静止开始沿轨道下滑,与静止在轨道BC段上质量为km的小球发生碰撞,碰撞前后两小球的运动方向处于同一水平线上。
(1)若两小球碰撞后粘连在一起,求碰后它们的共同速度;
(2)若两小球在碰撞过程中无机械能损失
a.为使两小球能发生第二次碰撞,求k应满足的条件;
b.为使两小球仅能发生两次碰撞,求k应满足的条件。
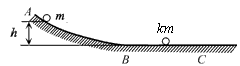
参考答案:解:(1)设质量为m的小球碰撞前的速度为v0,根据机械能守恒定律有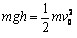 ①
①
设两小球碰后的共同速度为V,根据动量守恒定律有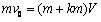 ②
②
解得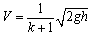
(2)a.取水平向右方向为正方向,设碰后m与km的速度分别为v1与V1,根据动量守恒定律和机械能守恒定律有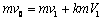 ③
③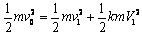 ?④
?④
解得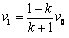 ⑤,
⑤,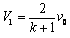 ⑥
⑥
两小球若要发生第二次碰撞,需要v1<0,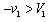 ⑦
⑦
由⑤⑥⑦解得:k>3 ⑧
b.对于第二次碰撞,设v2与V2分别为m与km碰后的速度,由动量守恒和机械能守恒有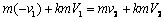 ?⑨
?⑨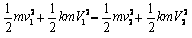 ?⑩
?⑩
由⑤⑥⑧⑨解得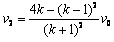
,
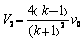
只要满足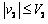 ,两球一定不会相碰
,两球一定不会相碰
由⑧解得
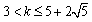
本题解析:
本题难度:困难