时间:2019-06-23 22:47:53
1、选择题 如图所示,质量为m的小球从距离地面高H的A点由静止开始释放,落到地面上后又陷入泥潭中,由于受到阻力作用到达距地面深度为h的B点速度减为零.不计空气阻力,重力加速度为g.关于小球下落的整个过程,下列说法中正确的有( )
A.以地面为重力势能零点,小球的机械能减少了mgH
B.小球克服阻力做的功等于小球机械能的减少量
C.小球所受阻力的冲量等于小球重力的冲量
D.若小球所受阻力恒定,阻力大小与重力大小之比为H:h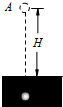
参考答案:A、从静止开始释放到落到地面,应用动能定理:mgH=Ek
小球陷入泥中的过程,根据动能定理:mgh-Wf=0-Ek
故Wf=mgh+Ek=mgh+mgH,克服阻力做的功等于小球机械能的减少量
故机械能减少了mgh+mgH,故A错误,B正确;
C、小球从下落到陷入的正个过程,受重力和阻力作用,动量的变化量为零,故小球所受阻力的冲量等于小球重力的冲量,故C正确;
D、由A分析知:Wf=mgh+mgH,即fh=mgh+mgH
故f:mg=h+Hh,故D错误
故选:BC
本题解析:
本题难度:一般
2、选择题 如图所示,一个物体以速度v冲向与竖直墙壁相连的轻质弹簧,墙壁和物体间的弹簧被物体压缩,在此过程中以下说法正确的是( )
A.物体对弹簧做的功与弹簧的压缩量成正比
B.物体向墙壁运动相同的位移,弹力做的功不相等
C.弹力做正功,弹簧的弹性势能减小
D.弹簧的弹力做负功,弹性势能增加
参考答案:弹簧弹力F=K△x,力做功表达式W=F△x=k△x2,可见物体对弹簧做的功与弹簧的压缩量平方成正比,故A错误;
B、物体向墙壁运动相同的位移,弹力大小不同,故弹力做功不相等,B正确;
C、物体向左运动,弹力方向向右,故弹力做负功,弹簧的弹性势能增加,C错误D正确;
故选:BD.
本题解析:
本题难度:一般
3、计算题 (2).(9分)如图所示,在光滑绝缘水 平面上有两个带电小球 、
、 ,质量分别为3m和m,小球
,质量分别为3m和m,小球 带正电q,小球
带正电q,小球 带负电-2q,开始时两小球相距s0,小球
带负电-2q,开始时两小球相距s0,小球 有一个水平向右的初速度v0,小球
有一个水平向右的初速度v0,小球 的初速度为零,若取初始状态下两小球构成的系统的电势能为零,试证明:当两小球的速度相同时系统的电势能最大,并求出该最大值;
的初速度为零,若取初始状态下两小球构成的系统的电势能为零,试证明:当两小球的速度相同时系统的电势能最大,并求出该最大值;
参考答案:
本题解析:(1)由于两小球构成的系统合外力为零,设某状态下两小球的速度分别为 和
和 ,由动量守恒定律得
,由动量守恒定律得  ?(1) (2分)
?(1) (2分)
所以,系统的动能减小量为? ?(2) (2分)
?(2) (2分)
由于系统运动过程中只有电场力做功,所以系统的动能与电势能之和守恒,考虑到系统初状态下电势能为零,故该状态下的电势能可表为 ?(3) (1分)
?(3) (1分)
联立(1)、(3)两式,得  ?(4)(1分)
?(4)(1分)
由(4)式得:当  ?(5) (1分)
?(5) (1分)
时,系统的电势能取得最大值,而将(5)式代入(1)式,得  ?(6)(1分)?
?(6)(1分)?
即当两小球速度相同时系统的电势能最大,最大值为 ?(7) (1分)
?(7) (1分)
本题难度:一般
4、选择题 如图所示,摆球原来处于它的平衡位置O点,后来摆球在水平恒力F的作用下,沿着圆弧运动。摆球经过P点时,它所受的切向合外力恰好为零,这时撤去拉力F,则 
[? ]
A.撤除F后,摆球的最大偏角大于图示的θ
B.摆线的拉力对摆球不做功
C.摆球从O到P的重力势能增量小于F对摆球做的功
D.从O到P摆球重力势能的增量等于F对摆球做的功
参考答案:ABC
本题解析:
本题难度:一般
5、简答题 一个竖直放置的光滑圆环,半径为 ,
, 、
、 、
、 、
、 分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图4所示.一个小球从与
分别是其水平直径和竖直直径的端点.圆环与一个光滑斜轨相接,如图4所示.一个小球从与 点高度相等的
点高度相等的 点从斜轨上无初速下滑.试求:
点从斜轨上无初速下滑.试求:
小题1:过 点时,对轨道的压力
点时,对轨道的压力 多大?
多大?
小题2:小球能否过 点,如能,在
点,如能,在 点对轨道压力
点对轨道压力 多大?如不能,小球于何处离开圆环?
多大?如不能,小球于何处离开圆环?
参考答案:
小题1: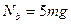
小题2: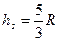
故小球经过圆环最低点 时,对环的压力为
时,对环的压力为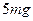 .小球到达高度为
.小球到达高度为 的
的 点开始脱离圆环,做斜上抛运动.
点开始脱离圆环,做斜上抛运动.
本题解析: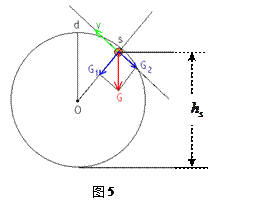
小题1:小球在运动的全过程中,始终只受重力 和轨道的弹力
和轨道的弹力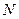 .其中,
.其中, 是恒力,而
是恒力,而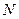 是大小和方向都可以变化的变力.但是,不论小球是在斜轨上下滑还是在圆环内侧滑动,每时每刻所受弹力方向都与即时速度方向垂直.因此,小球在运动的全过程中弹力不做功,只有重力做功,小球机械能守恒.
是大小和方向都可以变化的变力.但是,不论小球是在斜轨上下滑还是在圆环内侧滑动,每时每刻所受弹力方向都与即时速度方向垂直.因此,小球在运动的全过程中弹力不做功,只有重力做功,小球机械能守恒.
从小球到达圆环最低点 开始,小球就做竖直平面圆周运动.小球做圆周运动所需的向心力总是指向环心
开始,小球就做竖直平面圆周运动.小球做圆周运动所需的向心力总是指向环心 点,此向心力由小球的重力与弹力提供.
点,此向心力由小球的重力与弹力提供.
(1)因为小球从 到
到 机械能守恒
机械能守恒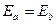 ,所以
,所以 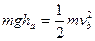 ?①
?① ?②
?② ?③
?③
解①②③得?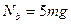
小题2:小球如能沿圆环内壁滑动到 点,表明小球在
点,表明小球在 点仍在做圆周运动,则
点仍在做圆周运动,则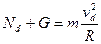 ,可见,
,可见, 是恒量,随着
是恒量,随着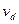 的减小
的减小 减小;当
减小;当 已经减小到零(表示小球刚能到达
已经减小到零(表示小球刚能到达 )点,但球与环顶已是接触而无挤压,处于“若即若离”状态)时,小球的速度是能过
)点,但球与环顶已是接触而无挤压,处于“若即若离”状态)时,小球的速度是能过 点的最小速度.如小球速度低于这个速度就不可能沿圆环到达
点的最小速度.如小球速度低于这个速度就不可能沿圆环到达 点.这就表明小球如能到达
点.这就表明小球如能到达 点,其机械能至少应是
点,其机械能至少应是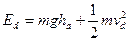 ,但是小球在
,但是小球在 点出发的机械能仅有
点出发的机械能仅有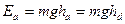 <
<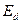 因此小球不可能到达
因此小球不可能到达 点.
点.
又由于 ,
,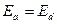
即
因此,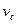 >0,小球从
>0,小球从 到
到 点时仍有沿切线向上的速度,所以小球一定是在
点时仍有沿切线向上的速度,所以小球一定是在 、
、 之间的某点
之间的某点 离开圆环的.设半径
离开圆环的.设半径 与竖直方向夹
与竖直方向夹 角,则由图可见,小球高度
角,则由图可见,小球高度 ?④
?④
根据机械能守恒定律,小球到达 点的速度
点的速度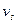 应符合:
应符合: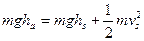 ?⑤
?⑤
小球从 点开始脱离圆环,所以圆环对小球已无弹力,仅由重力
点开始脱离圆环,所以圆环对小球已无弹力,仅由重力 沿半径方向的分力提供向心力,即
沿半径方向的分力提供向心力,即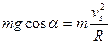 ?⑥
?⑥
解④⑤⑥得?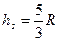
故小球经过圆环最低点 时,对环的压力为
时,对环的压力为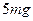 .小球到达高度为
.小球到达高度为 的
的 点开始脱离圆环,做斜上抛运动.
点开始脱离圆环,做斜上抛运动.
本题难度:一般