时间:2019-06-23 22:27:24
1、计算题 如图2-1所示，轻质长绳水平地跨在相距为2L的两个小定滑轮A、B上，质量为m的物块悬挂在绳上O点，O与A、B两滑轮的距离相等。在轻绳两端C、D分别施加竖直向下的恒力F=mg。先托住物块，使绳处于水平拉直状态，由静止释放物块，在物块下落过程中，保持C、D两端的拉力F不变。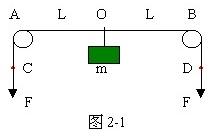
（1）当物块下落距离h为多大时，物块的加速度为零？
（2）在物块下落上述距离的过程中，克服C端恒力F做功W为多少？
（3）求物块下落过程中的最大速度Vm和最大距离H？
参考答案：（1）当物块所受的合外力为零时，加速度为零，此时物块下降距离为h。因为F恒等于mg，所以绳对物块拉力大小恒为mg，由平衡条件知：2θ=120°，所以θ=60°，由图2-2知：h=L×tg30°=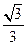
L [1]（4分）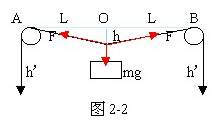
2）当物块下落h时，绳的C、D端均上升h’，由几何关系可得：h’=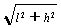
-L? [2]?
克服C端恒力F做的功为：W="F*h’" [3] （2分）
由[1]、[2]、[3]式联立解得：W=（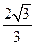
-1）mgL?（2分）
（3）出物块下落过程中，共有三个力对物块做功。重力做正功，两端绳子对物块的拉力做负功。两端绳子拉力做的功就等于作用在C、D端的恒力F所做的功。因为物块下降距离h时动能最大。由动能定理得：mgh-2W=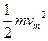
? [4]?（2分）
将[1]、[2]、[3]式代入[4]式解得：Vm=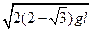
?（1分）
当物块速度减小为零时，物块下落距离达到最大值H，绳C、D上升的距离为H’。由动能定理得：mgH-2mgH’=0，又H’=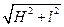
-L，联立解得：H=
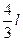。（3分）
本题解析：略
本题难度：一般
2、简答题 硅光电池是一种可将光能转换为电能的器件．某同学用图（1）所示电路探究硅光电池的路端电压U与总电流I的关系．图中R0为已知定值电阻，电压表视为理想电压表．
（1）若电压表V2的读数为U0，则I=______．
（2）实验一：用一定强度的光照射硅光电池，调节滑动变阻器，通过测量得到该电池的U-I曲线a．见图（2）所示，由此可知电池内阻______?（填“是”或“不是”）常数，电动势为______V．
（3）实验二：减小实验一中光的强度，重复实验，测得U-I曲线b，见图（2）所示．若取实验一中的路端电压为1.5V，保持外电路中电阻不变，则实验二中外电路消耗的电功率为______mW（计算结果保留两位有效数字）．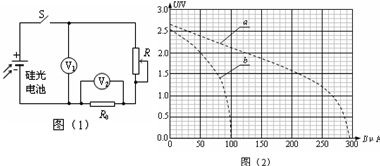
参考答案：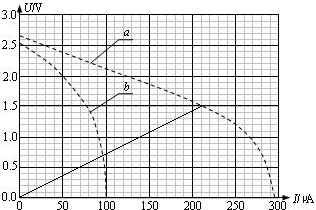
（1）若电压表V2的读数为U0，则I=U0R0．
（2）根据闭合电路欧姆定律U=E-Ir可知，电池的U-I曲线的斜率大小等于电源的内阻，纵轴截距等于电池的电动势，由图看出，该电池的U-I图线是曲线，则知该电池的内阻不是常数，电动势为E=2.67V．
（3）实验一中的路端电压为U1=1.5V时电路中电流为I1=0.21mA，连接a中的点（0.21mA、1.5V）和坐标原点，
此直线为此时对应滑动变阻器阻值的外电路电阻（定值电阻）的U-I图，和图线b的交点为实验二中的路端电压和电路电流，由b可知：电流和电压分别为I=97μA、U=0.7V，
则外电路消耗功率为P=UI=97×10-3mA×0.7V≈0.070mW．
答：（1）U0R0（2）不是；2.67．（3）0.070
本题解析：
本题难度：一般
3、计算题 (10分)在如图所示的电路中,已知电源电动势E="3" V,内电阻r=1Ω,电阻R1=2Ω,滑动变阻器R的阻值可连续增大,问: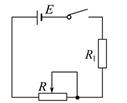
(1)当R多大时,R消耗的功率最大?最大功率为多少? 当R消耗功率最大时电源的效率是多少？
(2)当R多大时,R1消耗的功率最大?最大功率为多少?
(3)当R为多大时，电源的输出功率最大？最大为多少？
参考答案：3 Ω 0.75W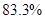 
0 2W 0 2W
本题解析： (1)把R1视为内电路的一部分,则当R=R1+r="3" Ω时,R消耗的功率最大,其最大值为: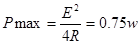
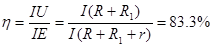
(2)对固定电阻R1,当电路的电流最大时其消耗的功率最大,此时R=0,所以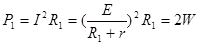
(3) R=0时电源的输出功率最大
考点：本题考查电路的计算.
本题难度：一般
4、选择题 如图甲所示，一个圆形线圈的匝数n=100，线圈面积S=200cm2，线圈的电阻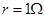
，线圈外接一个阻值
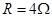的电阻，把线圈放入一方向垂直线圈平面向里的匀强磁场中，磁感应强度随时间变化规律如图已所示．下列说法中正确的是
A．电阻R两端的电压保持不变
B．初始时刻穿过线圈的磁通量为0.4Wb
C．线圈电阻r消耗的功率为4×10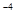
W
D．前4s内通过R的电荷量为4×10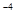C
参考答案：AC
本题解析：根据法拉第电磁感应定律可知，磁通量的变化率恒定，所以电动势恒定，则电阻两端的电压恒定，故A正确；初始时刻磁感应强度等于0.2T，穿过线圈的磁通量为0.004Wb，B错误；由法拉第电磁感应定律：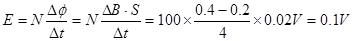
，由闭合电路欧姆定律，可知电路中的电流为I=E/(R+r)=0.02A，所以线圈电阻r消耗的功率
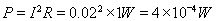，故C正确；前4s内通过R的电荷量
，D错误；故选AC。
考点：法拉第电磁感应定律；闭合电路的欧姆定律．
本题难度：一般
5、简答题 相隔一定距离的A，B两球质量相等，假定它们之间存在恒定的斥力作用．原来两球被按住，处在静止状态．现突然松开两球，同时给A球以速度v0，使之沿两球连线射向B球，B球初速为零．若两球间的距离从最小值(两球未接触)到刚恢复到原始值所经历的时间为t0．求B球在斥力作用下的加速度．
参考答案：
本题解析：
以m表示每个球的质量，F表示恒定斥力，L表示两球间原始距离，松开后，A球做初速为v0的匀减速运动，B球做初速为零的匀加速运动．设在两球间距由L变小到恢复到L的过程中，A球的路程为L1，B球的路程为L2；刚恢复到原始长度时，A球的速度为v1，B球的速度为v2．由动量守恒定律有mv0＝mv1＋mv2．由功能关系得FL1＝
－
，FL2＝
．由于初、末态两球间距相等，故有L1＝L2，由以上各式解得v2＝v0．当两球速度相等时，距离最小，设此时球速为u，由动量守恒定律得mv0＝(m＋m)u，设a为B球的加速度，则有v2＝u＋at0，得a＝．
本题难度：一般