时间:2019-06-23 22:22:55
1、选择题 如图所示,质量为m的小球在竖直平面内的光滑圆轨道上做圆周运动。圆半径为R,小球经过圆环最高点时刚好不脱离圆轨道,则其通过最高点时
A.小球对圆环的压力大小等于mg
B.小球只受重力
C.小球的线速度大小等于
D.小球的向心加速度大小等于g
参考答案:BCD
本题解析:小球经过圆环最高点时刚好不脱离圆轨道,这时小球对圆环没有作用力,只有重力提供小球做圆周运动的向心力,有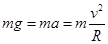 ,所以向心加速度大小等于g, 小球的线速度大小等于
,所以向心加速度大小等于g, 小球的线速度大小等于
本题难度:一般
2、选择题 某物体作匀速圆周运动,在其运动过程中,不发生变化的物理量是( )
A.线速度
B.角速度
C.向心加速度
D.合外力
参考答案:B
本题解析:A、在匀速圆周运动的过程中,线速度的大小不变,方向时刻改变;错误
B、在匀速圆周运动的过程中,角速度的大小和方向都不变;B正确
C、在匀速圆周运动的过程中,向心加速度的大小不变,方向始终指向圆心,方向是变化的;错 误
D、在匀速圆周运动的过程中,合外力的大小不变,方向始终指向圆心;错误
故选B
考点:描述匀速圆周运动的物理量
点评:如果说一个矢量不发生变化,不但是大小不变,方向也得不变。做匀速圆周运动的物体,向心加速度和向心力的方向始终指向圆心,方向是变化的。
本题难度:一般
3、选择题 将一物体由地面竖直上抛,如果不计空气阻力,物体能够达到的最大高度为H,当物体在上升过程中某一位置,它的动能是重力势能的2倍(以地面作为重力势能零势能面),则这一位置的高度是(?)
A. H
H
B. H
H
C. H
H
D. H
H
参考答案:C
本题解析:分析:不计空气阻力说明机械能守恒,利用初速度条件与某一高度时重力势能是动能两倍求解.
解答:解:依题意知物体机械能守恒,初动能W1=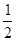 m
m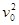 =mgH,
=mgH,
动能是重力势能的2倍时,离地面高度设为h,则此时重力势能为mgh
mgh+Ek=mgh+2mghW1= mgH,h=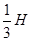
故选C
点评:此题是针对机械能守恒的专项训练,要善于利用和挖掘条件.
本题难度:简单
4、计算题 (8分)如图所示,用长为L的细绳拴住一个质量为m的小球,当小球在水平面内做匀速圆周运动时,细绳与竖直方向成θ角,求:
(1)细绳对小球的拉力;
(2)小球做匀速圆周运动的周期。
参考答案:(1) 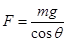 (2)
(2) 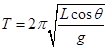
本题解析:对小球进行受力分析(图略),并分解拉力F,由牛顿第二定律可知: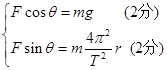
而由几何关系可知: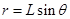 (2分)
(2分)
解得: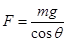 (1分)
(1分) 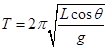 (1分)
(1分)
考点:本题考查圆周运动与向心力。
本题难度:一般
5、选择题 某同学向海中投掷一小石子,石子在空中画出一条优美的抛物线落入海水中,若不计空气阻力,下述说法正确的是( )
A.石子在空中只有重力做功
B.石子在空中运动过程中,石子速度一直增大
C.石子在空中重力和手给它做功
D.石子在空中运动过程中,石子机械能保持不变
参考答案:AD
本题解析:略
本题难度:简单