时间:2019-05-21 05:28:45
1、选择题 如图所示，一光滑斜面的直角点A处固定一带电荷量为＋q、质量为m的绝缘小球，另一同样小球置于斜面顶点B处，已知斜面长为L，现把上部小球从B点由静止自由释放，球能沿斜面从B点运动到斜面底端C处，求：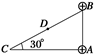
(1)小球从B处开始运动到斜面中点D处时的速度；
(2)小球运动到斜面底端C处时，球对斜面的压力是多大？
参考答案：(1)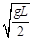 
(2) 
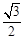mg－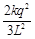
本题解析：由于小球沿斜面下滑过程中所受电场力为变力，因此不能用功的定义来求解，只能用动能定理求解
(1)由题意知：小球运动到D点时，由于AD＝AB，所以有电势φD＝φB，即UDB＝φD－φB＝0①
则由动能定理得：mg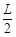
sin30°＝
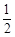mv
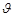－0②
联立①②解得：vD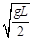＝③
(2)当小球运动至C点时，对球受力分析如图所示，则由平衡条件得：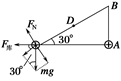
FN＋F库sin30°＝mgcos30°④
由库仑定律得：
F库＝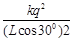
⑤
联立④⑤得：
FN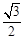＝mg－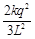
由牛顿第三定律得：FN′＝FN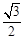＝mg－.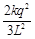
本题难度：一般
2、计算题 （12分）有带电平行板电容器竖直放置，如图9示。板间距d=0.1m、板间电势差U=1000V。现从A处以速度vA=3m/s水平向左射出一带正电的小球（质量m=0.02g、电量为q=10-7C）经过一段时间后发现小球打在A点正下方的B处，（g=10m/s2）求：
（1）分别从水平方向和竖直方向定性分析小球从A到B的过程中，小球的运动情况？
（2）A、B间的距离？(小球由A到B的过程中，不会碰到左极板。)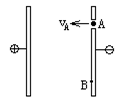
参考答案：(1)水平方向小球开始向左做初速度为vA匀减速运动，速度变为零后向右做匀加速运动，直到达到B点，过程中加速度不变，由电场力提供外力。?
竖直方向小球向下做初速为零匀加速运动，直到达到B点，重力提供外力。?
（2）7.2cm
本题解析：(1)水平方向小球开始向左做初速度为vA匀减速运动，速度变为零后向右做匀加速运动，直到达到B点，过程中加速度不变，由电场力提供外力。?
竖直方向小球向下做初速为零匀加速运动，直到达到B点，重力提供外力。?
（2）水平方向：电场力为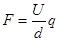
?加速度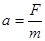
?
小球向左运动到最远的时间为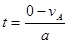
=0.06S?
在这段时间内向右运动的距离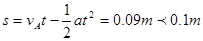
，不会撞倒左壁。
小球达到B点所用时间为T=2t?
竖直方向下落距离即为所求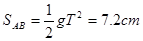
?
本题考查带电粒子在电场中的加速问题，由力的独立作用原理可知水平方向小球开始向左做初速度为vA匀减速运动，速度变为零后向右做匀加速运动，直到达到B点，过程中加速度不变，由电场力提供外力，竖直方向小球向下做初速为零匀加速运动，直到达到B点，重力提供外力，在水平方向上由电场力提供加速度，运动到最远距离速度为零，由运动学公式可求得加速度与运动时间，从而求得位移大小，同理在竖直方向由自由落体运动求解
本题难度：一般
3、计算题 如图所示，在真空中的竖直平面内，用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B，A球的电荷量为+4q，B球的电荷量为—3q，组成一带电系统。虚线MN与PQ平行且相距3L，开始时PQ恰为杆的中垂线。在MN与PQ间加竖直向上的匀强电场，恰能使带电系统静止不动。现使电场强度突然加倍（已知当地重力加速度为g），求：
（1）B球刚进入电场时的速度v1的大小；
（2）B球的最大位移及从开始静止到最大位移处B球电势能的变化量；
（3）带电系统运动的周期T。
参考答案：（1）设带电系统静止时电场强度为E，有2mg =4qE，解得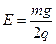
?①
电场强度加倍后，从开始静止到B进入电场，根据动能定理有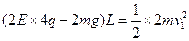
?②
联立①②得B球刚进入电场时的速度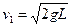
（2）设B球在电场中的最大位移为s，经分析知A球向上越过了MN，根据动能定理有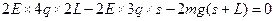
解得s=1.2L?故B球的最大位移s总=2.2L
电场力对B球做功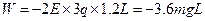
则B球电势能增加3.6mgL
（3）带电系统向上运动分为三阶段，第一阶段匀加速运动，据牛顿第二定律有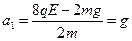
，运动时间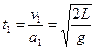
；
第二阶段匀减速运动，同理可得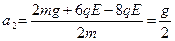
设A球出电场时速度为v2，根据运动学公式有：
，解得
，
；
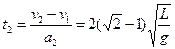第三阶段匀减速运动，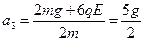
，
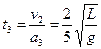
则运动周期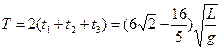
本题解析：略
本题难度：一般
4、计算题 在场强为E＝0.2 N/C的竖直向下匀强电场中有一块水平放置的接地金属板，在金属板的正上方放置一块厚铅板A，A的下方中心处离地高为h＝0.45 m处有一个很小的放射源，它可向各个方向均匀地释放质量为m＝2×10－23 kg、电量为q＝+10－17 C、初速度为v0＝1000 m/s的带电粒子。粒子重力不计，粒子最后落在金属板上。试求：
小题1:粒子下落过程中电场力做的功。
小题2:粒子到达金属板所需的最长时间。
小题3:粒子最后落在金属板上所形成的图形及面积的大小。
参考答案：
小题1:W＝9?1019 J
小题2:a＝105 m/s2? t＝3?103 s?
小题3:圆形? R＝3m? S＝9p（或28.26）m2
本题解析：小题1:电场对所有粒子做功一样多，即W=Eqh=0.2×10-17×0.45=9×10-19 J
小题2:水平抛出的粒子由于没有竖直分速度，到达金属板时的时间最长，由牛顿第二定律可知：a=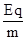
=105 m/s2
由h=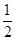
at2解得：t=
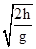=3×10-3 s；
小题3:（3）由题意可知各方向沿水平方向射出的粒子到达最远距离，故在金属板上形成圆形；由r=vt可知；
半径为：r=1000m/s×3×10-3 s=3m； S=πr2=9πm2
本题难度：简单
5、计算题 如图所示的电路中，三个电阻阻值均为R，电源内阻不计。两金属板间的距离为d，当开关K闭合时，一质量为m、电量为q的带电油滴从高处由静止下落经上板中央小孔后，落到两板间的匀强电场中时做匀速运动。开关断开后，仍使该油滴从同一位置由静止落下，恰好不能碰到下板，忽略空气对油滴的浮力和阻力，重力加速度为g。求：
（1）油滴开始下落时离上板的高度H；
（2）开关断开后，油滴下落过程的总时间t。
参考答案：（1）H=2d（2）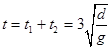
本题解析：（1）设电源电动势为U，K闭合时，有mg=Eq，E=U/3d。
K断开后，有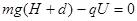
， 得H=2d。? 4分
（2）进入电场前，有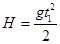
，
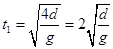，加速和减速过程平均速度相同，
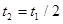，则总时间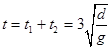?。? 4分
点评：关键是对粒子在进入前和进入后的运动性质把握到位，然后根据直线运动规律解题，难度适中
本题难度：一般