时间:2019-05-21 05:02:28
1、简答题 一辆装砂的小车的总质量为M,正在光滑的水平面上以速度v匀速前进,突然车底开始漏砂子,不断有砂子落到地面上.求当漏掉的砂子质量为m时,小车的速度.
参考答案:v
本题解析:漏掉的砂子在离开车子后,其速度跟小车相同,由动量守恒定律得:
Mv=(M-m)v′+mv′
小车的速度v′=v,即在漏出质量为m的砂子后,小车的速度不变.
本题难度:简单
2、选择题 目前,载人宇宙飞船返回舱的回收常采用强制减速的方法,整个回收过程可以简化为这样几个主要的阶段:第一阶段,在返回舱进入大气层的过程中,返回舱在大气阻力和重力的共同作用下匀速下降.第二阶段,返回舱到了离地一定高度时打开降落伞使返回舱以较低的速度匀速落下.第三阶段,在返回舱接近地面时点燃反冲火箭使返回舱做减速运动直至落地.关于这三个阶段中返回舱机械能及动量的变化情况,以下说法正确的是(?)
A.第一阶段返回舱机械能的减少量等于返回舱所受外力做功的代数和
B.第二阶段返回舱机械能的减少量等于返回舱克服大气阻力做的功
C.第三阶段返回舱动能的变化量等于反冲火箭对返回舱做的功
D.第三阶段返回舱动量的变化量等于反冲火箭对返回舱的冲量
参考答案:B
本题解析:根据功能原理知,返回舱在第一、第二阶段机械能的减少量等于它克服空气阻力做的功,不包括重力的功,选项A错B对;在第三阶段,其动量的变化量等于合外力的冲量,不仅是反冲火箭的冲量;其动能的变化量等于合外力对它做的功,不仅是反冲火箭的功,选项C、D错误.
本题难度:简单
3、选择题 在光滑水平面上,一物体以速度v运动.一块橡皮泥从空中自由下落到物体上,与物体粘在一起,则橡皮泥与物体组成的系统在水平方向的总动量和物体最终速度的变化分别为( )
A.增大,不变
B.减小,不变
C.不变,减小
D.不变,增大
参考答案:在此作用过程中,水平方向的动量守恒,所以水平方向总动量不变;设物体的质量为M,橡皮泥的质量为m,它们的共同速度为vt
则Mv=(M+m)vt
得vt=MM+mv<v
所以速度变小了
故选C
本题解析:
本题难度:简单
4、选择题 如图所示,小车与木箱紧挨着静放在光滑的水平冰面上,现有一男孩站在小车上用力向右迅速推出木箱,关于上述过程,下列说法中正确的是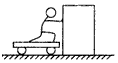
[? ]
A.男孩和木箱组成的系统动量守恒
B.小车与木箱组成的系统动量守恒
C.男孩、小车与木箱三者组成的系统动量守恒
D.木箱的动量增量与男孩、小车的总动量增量相同
参考答案:C
本题解析:
本题难度:简单
5、简答题 质量为m=200g的子弹,以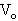 =200m/s的速度水平射向质量为M=0.8kg的木块.若将木块固定,子弹穿出木块后的速度为V=100m/s;若将木块放在光滑水平地面上,仍以
=200m/s的速度水平射向质量为M=0.8kg的木块.若将木块固定,子弹穿出木块后的速度为V=100m/s;若将木块放在光滑水平地面上,仍以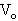 =200m/s的水平速度将子弹射向木块,则子弹和木块的速度将各是多少?
=200m/s的水平速度将子弹射向木块,则子弹和木块的速度将各是多少?
参考答案:
20m/s? ,120m/s
本题解析:
本题难度:一般