时间:2019-05-21 04:14:39
1、计算题 如图所示,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面夹角θ=30°,导轨电阻不计。磁感应强度为B=2T的匀强磁场垂直导轨平面向上,长为L=0.5m的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨电接触良好,金属棒ab的质量m=1kg、电阻r=1Ω。两金属导轨的上端连接右端电路,灯泡电阻RL=4Ω,定值电阻R1=2Ω,电阻箱电阻R2=12Ω,重力加速度为g="10" m/s2,现闭合开关,将金属棒由静止释放,下滑距离为s0=50m时速度恰达到最大,试求: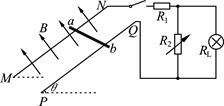
(1)金属棒下滑的最大速度vm;
(2)金属棒由静止开始下滑2s0的过程中整个电路产生的电热Q。
参考答案:(1)30m/s(2)50J
本题解析:(1)当金属棒匀速下滑时速度最大,设最大速度为vm,达到最大时,则根据平衡条件有
mgsinθ=F安
又 F安=ILB,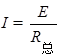 ,E=BLvm
,E=BLvm
R总=R1+r+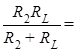 6Ω
6Ω
联立解得最大速度:vm=30m/s
(2)由能量守恒知,mg?2S0sin30°=Q+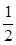 mvm2
mvm2
解得,Q=50J
考点:法拉第电磁感应定律;能量守恒定律;
本题难度:困难
2、选择题 如图所示,用长度La:Lb=2:1的同种导线做成圆环a、b,并在A、C处相连,当均匀变化的磁场垂直穿过a环时,环内电流为I1,A、C间电压为U1;若同样磁场穿过b环,环内电流为I2,A、C间电压为U2,则( )
A.I1:I2=4:1
B.I1:I2=2:1
C.U1:U2=2:1
D.U1:U2=4:1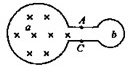
参考答案:A、B、用长度La:Lb=2:1的同种导线做成圆环a、b,故两个环的半径之比为2:1,面积之比为4:1;
根据电阻定律公式R=ρLS,左右两侧的电阻之比为:R1:R2=2:1;
根据法拉第电磁感应定律,感应电动势:E=nS△B△t∝S;故两次的电动势之比为4:1;
根据闭合电路欧姆定律公式I=ER总,感应电流之比为4:1;
故A正确,B错误;
C、D、路端电压U=IR,第一次外电阻是右侧电阻,第二次外电阻是左侧电阻,故两次的路端电压之比为:
U1U2=I1R2I2R1=4×11×2=21
故C正确,D错误;
故选:AC.
本题解析:
本题难度:一般
3、选择题 一个位于竖直平面内的正方形闭合导体框,其上、下两条边水平,从静止开始下落一定高度后,垂直穿越一个磁感线沿水平方向且与导体框平面垂直的有界匀强磁场区域,该区域上、下边界也水平。下图是自导体框开始下落到完全穿越磁场区域的过程中,导体框中的感应电流随时间变化的图像,其中肯定与实际不相符的是(忽略空气阻力的影响,导体框始终在竖直平面内平动)
[? ]
A.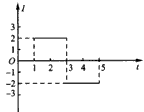
B.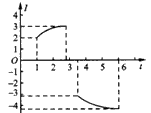
C.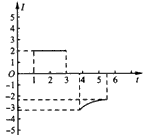
D.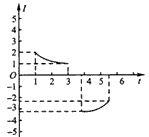
参考答案:BD
本题解析:
本题难度:一般
4、选择题 如图,匀强磁场垂直于正方形线框平面,且边界恰与线框重合,以相同速率匀速拉出线框,欲使ab间电势差最大,则应沿何方向拉出(? )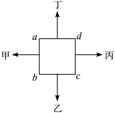
A.甲
B.乙
C.丙
D.丁
参考答案:C
本题解析:注意分清内、外电路,当ab两端电压为端电压时,其电势差最大,如图所示,Uab=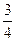 ε=
ε=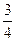 BLv,故应沿丙方向拉出.
BLv,故应沿丙方向拉出.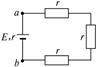
本题难度:一般
5、计算题 (8分)如图所示,边长为L、匝数为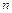 的正方形金属线框,它的质量为m、电阻为R,用细线把它悬挂于一个有界的匀强磁场边缘。金属框的上半部处于磁场内,下半部处于磁场外,磁场随时间的变化规律为B = kt。求:
的正方形金属线框,它的质量为m、电阻为R,用细线把它悬挂于一个有界的匀强磁场边缘。金属框的上半部处于磁场内,下半部处于磁场外,磁场随时间的变化规律为B = kt。求: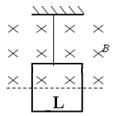
(1)线框中的电流强度为多大?
(2)t时刻线框受的安培力多大?
参考答案:(1)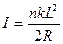
(2)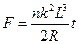
本题解析:
(1)线框中的电动势 ,电流为
,电流为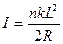
(2)安培力为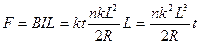
本题难度:简单