时间:2019-03-16 03:08:01
1、选择题 带电粒子以初速v0垂直电场方向进入平行金属板形成的匀强电场中,它离开时偏离原方向h,偏角为,下列说法中正确的是φ
粒子在电场中作类似平抛的运动
偏角φ与粒子的电量和质量无关
C.粒子飞过电场的时间,决定于极板长和粒子进入电场时的初速度
D.粒子偏移距离h,可用加在两极板上的电压控制
参考答案:ACD
本题解析:带电粒子在电场中只受垂直于初速度的电场力作用,所以做类平抛运动,A对;偏转角φ的正切tanφ=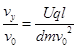 ,由关系式可知,偏转角与电量和质量都有关系,B错;飞出电场的时间t=l/v,所以C对;沿电场方向的偏转位移h=
,由关系式可知,偏转角与电量和质量都有关系,B错;飞出电场的时间t=l/v,所以C对;沿电场方向的偏转位移h=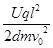 ,对同一粒子来说,可以由电压控制偏转距离,D对。
,对同一粒子来说,可以由电压控制偏转距离,D对。
本题难度:简单
2、计算题 (16分)如图,水平放置的平行板电容器,原来两极板不带电,上极板接地,它的极板长L=0.1 m,两极板间距离d=0.4 cm.有一束相同微粒组成的带电粒子流从两板中央平行于极板射入,由于重力作用微粒落到下板上.已知微粒质量为m=2×10-6 kg,电荷量为q=+1×10-8 C,电容器电容为C=10-6 F,g 取10 m/s2,求: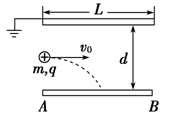
(1)为使第一个微粒的落点范围在下极板中点到紧靠边缘的B点之内,则微粒入射速度v0应为多少?
(2)若带电粒子落到AB板上后电荷全部转移到极板上,则以上述速度射入的带电粒子最多能有多少个落到下极板上?
参考答案:(1) 2.5 m/s<v0<5 m/s(2)600个
本题解析:(1)若第一个粒子落到O点,
由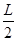 =v01t1? ---------2分
=v01t1? ---------2分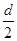 =
=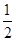 ?
?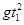 得v01=2.5 m/s ---------2分
得v01=2.5 m/s ---------2分
若落到B点,由L=v02t1 -------2分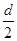 =
=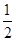
 得v02=5 m/s
得v02=5 m/s
故 2.5 m/s<v0<5 m/s.-----------2分
(2)由L=v01t,得t=4×10-2 s--------2分
由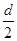 =
=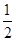 ?at2得a=2.5 m/s2-------------2分
?at2得a=2.5 m/s2-------------2分
由mg -qE=ma,E= ? ----------2分
? ----------2分
得Q=6×10-6C
所以n=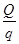 =600个.----------2分
=600个.----------2分
本题带电粒子在匀强电场中的偏转,如果粒子落在O点,由粒子所受电场力方向与速度方向垂直可知粒子做的是类平抛运动,由平抛运动规律可求得此时速度大小,如果粒子落在B点,由水平和竖直方向的分运动可求得此时速度大小,由此可知粒子初速度的取值范围,随着落在下极板的电荷越来越多,极板间的场强越来越大,由水平分速度先求的运动时间,再由竖直方向的匀加速直线运动求得加速度大小,由牛顿第二定律求得电场力大小,由E=U/d可求得电压大小,由电容器的电容公式可求得极板带电量,从而求得粒子个数
本题难度:一般
3、选择题 空间某区域存在着电场,电场线在竖直面上的分布如图所示,一个质量为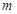 、电量为
、电量为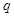 的小球在该电场中运动,小球经过A点时的速度大小为
的小球在该电场中运动,小球经过A点时的速度大小为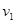 ,方向水平向右,运动至B点时的速度大小为
,方向水平向右,运动至B点时的速度大小为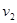 ,运动方向与水平方向之间夹角为
,运动方向与水平方向之间夹角为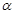 ,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是? (? )
,A、B两点之间的高度差与水平距离均为H,则以下判断中正确的是? (? )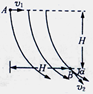
A.小球由A点运动至B点,电场力做的功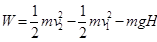
B.A、B两点间的电势差
C.带电小球由A运动到B的过程中,电场力对小球一定做正功
D.小球运动到B点时所受重力的瞬时功率为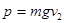
参考答案:A
本题解析:A、根据动能定理得: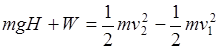 ,得到
,得到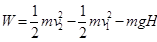 .故A正确;
.故A正确;
B、由公式W=qU,得到A、B两点间的电势差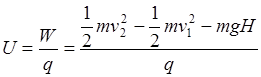 .故B错误.
.故B错误.
C、由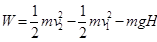 可知,当
可知,当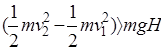 时,W>0,电场力做正功;当(
时,W>0,电场力做正功;当(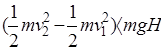 时,W<0,电场力负功.故C错误.
时,W<0,电场力负功.故C错误.
D、小球运动到B点时重力方向竖直向下,而小球的速度不是竖直向下,所以重力的瞬时功率P≠mgv2.故D错误.
故选A.
本题难度:简单
4、选择题 一质量为m的带电小球,在竖直方向的匀强电场中以初速度v0水平抛出,小球的加速度大小为2g/3,则小球在下落h高度过程中
[? ]
 mgh
mgh  mgh
mgh  mgh
mgh  mgh
mgh 参考答案:ABD
本题解析:
本题难度:一般
5、计算题 (11分)如图所示,真空中水平放置的两个相同极板Y和Y"长为L,相距d,足够大的竖直屏与两板右侧相距b.在两板间加上可调偏转电压U,一束质量为m、带电量为+q的粒子(不计重力)从两板左侧中点A以初速度v0沿水平方向射入电场且能穿出. 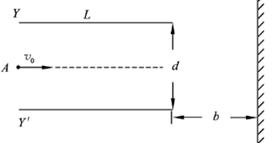
(1)证明粒子飞出电场后的速度方向的反向延长线交于两板间的中心O点;
(2)求两板间所加偏转电压U的范围;
(3)求粒子可能到达屏上区域的长度.
参考答案:(1)见解析(类平抛运动)(2)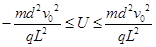 (3)
(3)
本题解析:(1)设粒子在运动过程中的加速度大小为a,离开偏转电场时偏转距离为y,沿电场方向的速度为vy,偏转角为θ,其反向延长线通过O点,O点与板右端的水平距离为x,如下图,则有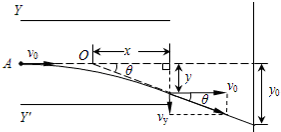
y=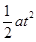 ?①
?①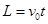 ?②
?②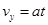 ?
? ?
?
联立可得?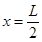 ?即粒子飞出电场后的速度方向的反向延长线交于两板间的中心.
?即粒子飞出电场后的速度方向的反向延长线交于两板间的中心.
(2)粒子在匀强电场中为类平抛运动,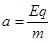 ? ③?
? ③?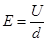 ?④
?④
由①②③④式解得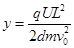
当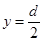 时,
时,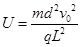 ?则两板间所加电压的范围?
?则两板间所加电压的范围?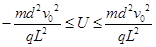
(3)当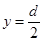 时,粒子在屏上侧向偏移的距离最大(设为y0),则
时,粒子在屏上侧向偏移的距离最大(设为y0),则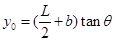
而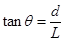
解得 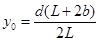
根据对称性,粒子可能到达屏上区域的长度为
本题难度:一般