时间:2019-03-16 03:01:33
1、选择题 如图所示，足够长的绝缘粗糙棒倾斜放置，棒上套有电量为q不会漏电的带正电小球，质量为m．现将此棒放入沿水平方向且相互垂直的匀强磁场和匀强电场中，小球由静止开始下滑的过程中（ ）
A．小球加速度逐渐减少直到为零
B．小球速度一直增大，直到最后匀速
C．小球受到摩擦力一直减少，直到速度最大时为零
D．小球所受洛伦兹力一直增大，直到最后不变
参考答案：对小球受力分析，受重力、摩擦力（可能有）、弹力（可能有）、洛伦兹力、电场力，如图所示：
A、根据牛顿第二定律，有：
ma=Gsinθ-qEcosθ-f…①
N+qvB=mgcosθ…②
其中：f=μN…③
由静到动，速度增加，故洛伦兹力增加，故合力先增加后减小，故加速度也是先增加后减小，故A错误；
B、加速度先增加后减小，与速度同方向，故速度先增加，最后匀速，故B正确；
C、根据②③式，小球受到的摩擦力是先减小后增加，故C错误；
D、速度先增加，最后不变，故洛伦兹力先增加，最后不变，故D正确；
故选：BD．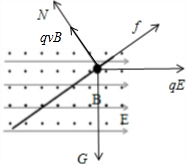
本题解析：
本题难度：一般
2、选择题 如图所示的虚线区域内，充满垂直于纸面向里的匀强磁场和竖直向下的匀强电场。一带电粒子a（不计重力）以一定的初速度由左边界的O点射入磁场、电场区域，恰好沿直线由区域右边界的O′点（图中未标出）穿出。若撤去该区域内的磁场而保留电场不变，另一个同样的粒子b（不计重力）仍以相同初速度由O点射入，从区域右边界穿出，则粒子b
[? ]
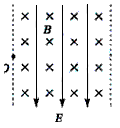
参考答案：C
本题解析：
本题难度：一般
3、计算题 如图所示，abcd为质量M＝2 kg的导轨，放在光滑绝缘的水平面，另有一根质量m＝0.6 kg的金属棒PQ平行于bc放在水平导轨上，PQ棒左边靠着绝缘的竖直立柱e、f（竖直立柱光滑，且固定不动），导轨处于匀强磁场中，磁场以
为界，左侧的磁场方向竖直向上，右侧的磁场方向水平向右，磁感应强度大小都为B＝0.8 T．导轨的bc段长l＝0.5 m，其电阻r＝0.4Ω，金属棒的电阻R＝0.2Ω，其余电阻均可不计．金属棒与导轨间的动摩擦因数m＝0.2．若在导轨上作用一个方向向左、大小为F＝2N的水平拉力，设导轨足够长，重力加速度g取
，试求：
（1）导轨运动的最大加速度；
（2）导轨的最大速度；
（3）定性画出回路中感应电流随时间变化的图线．
参考答案：（1）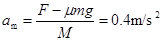
（2）
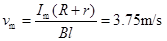（3）见解析
本题解析：解：导轨在外力作用下向左加速运动，由于切割磁感线，在回路中要产生感应电流，导轨的bc边及金属棒PQ均要受到安培力作用，PQ棒受到的支持力要随电流的变化而变化，导轨受到PQ棒的摩擦力也要变化，因此导轨的加速度要发生改变．导轨向左切割磁感线时，有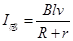
，① 导轨受到向右的安培力
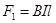，金属棒PQ受到向上的安培力
，导轨受到PQ棒对它的摩擦力
，根据牛顿第二定律，有F-BIl-?m（mg-BIl）＝Ma，即F-（1-m?）BIl-?mg＝Ma．②
（1）当刚拉动导轨时，v＝0，由①式可知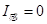
，则由②式可知，此时有最大加速度
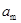，即．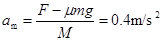
（2）随着导轨速度v增大，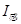
增大而a减小，当a＝0时，有最大速度
，从②式可得
，有
③ 将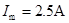
代入①式，得．
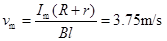（3）从刚拉动导轨开始计时，t＝0时，
，I＝0，当
时，v达到最大，I达到2.5 A，电流I随时间t的变化图线如图所示．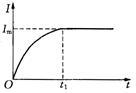
本题考查的是电磁感应定律和力学综合的相关问题，根据电磁感应定律和安培力的计算，利用牛顿第二定律计算出加速度；再根据运动学相关规律计算出最大电流，利用欧姆定律从而计算出导轨的最大速度；最后根据感应电流的变化画出图线；
本题难度：一般
4、选择题 在长方形abcd区域内有正交的电磁场，ab=bc/2=L，一带电粒子从ad的中点垂直于电场和磁场方向射入，恰沿直线从bc边的中点P射出，若撤去磁场，则粒子从C点射出；若撤去电场，则粒子将（重力不计）
[? ]
A．从b点射出
B．从b、P间某点射出
C．从a点射出
D．从a、b间某点射出
参考答案：C
本题解析：
本题难度：一般
5、计算题 （10分）如图所示，一倾角为θ=37o的绝缘斜面高度为h=3m，底端有一固定挡板，整个斜面置于水平向右匀强电场中，场强E=1×106N/C．现有一质量为m=0.2kg，电荷量为q=－1×10－6C的小物体，沿斜面顶端从静止开始下滑，小物体与斜面间的动摩擦因数为?=0.2，且小物体与挡板碰撞时不损失机械能(g=10m/s2,sin37o=0.6，cos37o=0.8）求：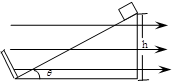
(1)小物体第一次与挡板碰撞前瞬间的动能；
(2)小物体从静止开始下滑到最后停止运动通过的总路程s．
参考答案：（1）
(2) 
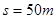
本题解析：对物块进行受力分析，如图所示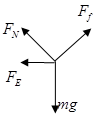 
解：（1）在运动过程中重力、静电力、摩擦力做功，
根据动能定理得?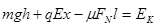
.......（2分）?
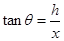?.....................................（1分）
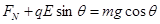? .......................................（2分）
联立代入数据得? .....................................（1分）
（2）整个过程中重力、静电力、摩擦力做功，
根据动能定理得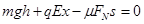
............（3分）?
代入数据得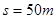.......（1分）
点评：本题难度中等，由问题可知本题考查的应该是功能关系的应用，此种类型题的分析，要先分析受力情况，再分析运动和做功情况，其中需要注意重力、电场力做功只与初末位置有关，而摩擦力做功与路径、路程有关
本题难度：一般