时间:2019-03-16 02:28:08
1、简答题 如图所示,有一对与电阻R=0.5Ω相连的平行导轨M和N,它们在同一水平面上,现加一匀强磁场,磁感应强度B=1T,磁场方向竖直向下,两导轨间距离L=0.05m,一质量m=0.01kg导体杆a、b垂直放在导轨上,ab杆和导轨电阻均不计,ab与导轨间动摩擦因数μ=0.1.今以F的水平恒定拉力拉ab,使它以恒定速度v=4m/s向右运动,(g=10m/s2)
求:(1)在图中标出通过电阻R中的电流方向;
(2)电阻R消耗的功率;
(3)水平的恒定拉力F的功率.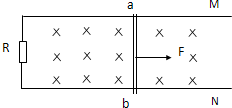
参考答案:解(1)由右手定则判断得知:ab棒中感应电流方向由b到a,则R中电流方向如图.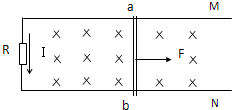
(2)感应电动势 E=BLv=0.2V
感应电流 I=ER=0.4A
故电阻R消耗的功率P=I2R=0.08W
(3)因导体杆匀速运动,则有:F=Ff+BIL=μmg+B2L2vR
代入数据解得:水平恒定拉力F=0.03N
由?PF=Fv
得?拉力F的功率PF=0.12W
答:
(1)在图中标出通过电阻R中的电流方向如图;
(2)电阻R消耗的功率是0.08W;
(3)水平的恒定拉力F的功率是0.12W.
本题解析:
本题难度:一般
2、选择题 如图所示,导体杆op可绕o轴沿半径为r的光滑的半圆形框架在匀强磁场中以角速度转动,磁感应强度为B,ao?间接有电阻R,杆和框架电阻不计,则所施外力的功率为( )
A.
| B2ω2r2 R |
| B2ω2r4 R |
| B2ω2r4 4R |
| B2ω2r4 8R |
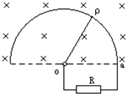
参考答案:因为OC是匀速转动的,根据能量的守恒可得,P外=P电=E2R,
又因为E=Br?ωr2,
联立解得:P外=B2ω2r44R,所以C正确.
故选C.
本题解析:
本题难度:简单
3、选择题 如图所示,三个电阻R1、R2、R3的阻值相同,允许消耗的最大功率分别为10W、10W、4W,则此电路允许消耗的最大功率为( ? )
A.12W
B.15W
C.16W
D.24W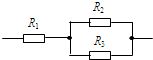
参考答案:B
本题解析:
本题难度:简单
4、选择题 有一个直流电动机,把它接入0.2V电压的电路时,电机不转,测得流过电动机的电流是0.4A;若把电动机接入2.0V电压的电路中,电动机正常工作,工作电流是1.0A.求
(1)电动机线圈的内阻
(2)电动机正常工作时的输出功率多大
(3)如果在发动机正常工作时,转子突然被卡住,电动机的发热功率是多大?
参考答案:(1)0.5Ω;(2)1.5W;(3)8W
本题解析:(1)接U =0.2V电压,电机不转,电流I =0.4A,
根据欧姆定律,线圈电阻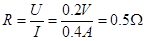 .
.
(2)当接U′=2.0V电压时,电流I′=1.0A,
故输入电功率P电=U′I′=2.0×1.0W=2.0W
热功率P热=I2R=12×0.5W=0.5W
故输出功率即机械功率P机=P电-P热=(2.0-0.5)W=1.5W.
(3)如果正常工作时,转子被卡住,则电能全部转化成内能故其发热功率
.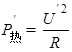
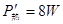
考点:电动机的计算;电功率.
本题难度:一般
5、简答题 如图所示,电源电动势E=6V,内阻r=0.5Ω,小电动机M的线圈电阻为0.5Ω,电阻R0=3Ω,电压表的示数为3V.求
(1)电源的输出功率
(2)电动机的输出功率.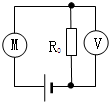
参考答案:(1)以电阻R0为研究对象,根据欧姆定律得到电路中电流为
? I=U0R0=33A=1A
则电源的输出功率P出=EI-I2r=6×1-12×0.5=5.5(W)
(2)电动机两端的电压U=E-U0-Ir=6-3-1×0.5=2.5(V)
电动机输入的电功率为P电=UI,内部发热为P热=I2RM,根据能量转化和守恒定律得,
电动机的输出功率P机=P电-P热=UI-I2RM=2.5×1-12×0.5(W)=2W
答:
(1)电源的输出功率是5.5W.?
(2)电动机的输出功率是2W.
本题解析:
本题难度:一般