时间:2019-03-16 01:46:52
1、实验题 某同学利用如图所示的装置进行验证动量守恒的实验: 
①先测出滑块A、B的质量M、m及滑块与桌面的动摩擦因数μ,查出当地的重力加速度g;
②用细线将滑块A、B连接,使A、B间的弹簧处于压缩状态,滑块B紧靠在桌边;
③剪断细线,测出滑块B做平抛运动落地时的水平位移为x1,滑块A沿桌面滑行距离为x2。
为验证动量守恒,写出还须测量的物理量及表示它的字母____________,如果动量守恒,须满足的关系是____________。
2、计算题 如图所示,轻弹簧的两端与质量均为2m的B、C两物块固定连接,静止在光滑水平面上,物块C紧靠挡板但不粘连.另一质量为m的小物块A以速度V0从右向左与B发生弹性正碰,碰撞时间极短可忽略不计.(所有过程都在弹簧弹性限度范围内)求: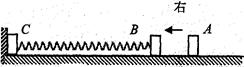
(1)A、B碰后瞬间各自的速度;
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比.
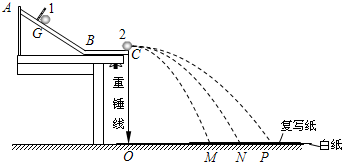
3、简答题 某同学用如图所示的装置,利用两个大小相同的小球做对心碰撞来验证动量守恒定律,图中AB是斜槽,BC是水平槽,它们连接平滑,O点为重锤线所指的位置.实验时先不放置被碰球2,让球1从斜槽上的某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹,重复10次.然后将球2置于水平槽末端,让球1仍从位置G由静止滚下,和球2碰撞.碰后两球分别在记录纸上留下各自的痕迹,重复10次.实验得到小球的落点的平均位置分别为?M、N、P.
(1)在此实验中,球1的质量为m1,球2的质量为m2,需满足m1______?m2(选填“大于”、“小于”或“等于”).
(2)被碰球2飞行的水平距离由图中线段______表示.
(3)若实验结果满足m1?
4、选择题 在光滑的水平面上有a、b两球,其质量分别是ma、mb,两球在t1时刻发生正碰,并且在碰撞过程中无机械能损失,两球在碰撞前后的速度图象如图所示.下列关系正确的是(?)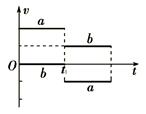
A.ma>mb
B.ma<mb
C.ma=mb
D.无法判断
5、填空题 如图1,用“碰撞实验器”可以验证动量守恒定律,即研究两个小球在轨道水平部分碰撞前后的动量关系.
①实验中,直接测定小球碰撞前后的速度是不容易的.但是,可以通过仅测量______(填选项前的符号),间接地解决这个问题.
A.小球开始释放高度h
B.小球抛出点距地面的高度H
C.小球做平抛运动的射程
②图10中O点是小球抛出点在地面上的垂直投影.实验时,先让入射球m1多次从斜轨上S位置静止释放,找到其平均落地点的位置P,测量平抛射程OP.
然后,把被碰小球m2静置于轨道的水平部分,再将入射球m1从斜轨上S位置静止释放,与小球m2相碰,并多次重复.
接下来要完成的必要步骤是______.(填选项前的符号)
A.用天平测量两个小球的质量m1、m2
B.测量小球m1开始释放高度h
C.测量抛出点距地面的高度H
D.分别找到m1、m2相碰后平均落地点的位置M、N
E.测量平抛射程OM,ON
③若两球相碰前后的动量守恒,其表达式可表示为______(用②中测量的量表示);若碰撞是弹性碰撞,那么还应满足的表达式为______(用②中测量的量表示).
④经测定,m1=45.0g,m2=7.5g,小球落地点的平均位置距O点的距离如图2所示.碰撞前、后m1的动量分别为p1与p1′,则p1:p1′=______:11;若碰撞结束时m2的动量为p2′,则p1′:p2′=11:______.
实验结果说明,碰撞前、后总动量的比值
| p1 ⑤有同学认为,在上述实验中仅更换两个小球的材质,其它条件不变,可以使被碰小球做平抛运动的射程增大.请你用④中已知的数据,分析和计算出被碰小球m2平抛运动射程ON的最大值为______cm. |