时间:2019-03-15 18:11:54
1、简答题 一足够长的矩形区域abcd内有磁感应强度为B，方向垂直纸面向里的匀强磁场，矩形区域的左边界ad宽为L，现从ad中点O垂直于磁场射入一带电粒子，速度大小为v0，方向与ad边夹角为θ=30°，如图所示．已知粒子的电荷量为q，质量为m（重力忽略不计）．
（1）若粒子带负电，且恰好能从d点射出磁场，求v0的大小；
（2）若粒子带正电，使粒子能从ab边射出磁场，求v0的取值范围，以及此范围内粒子在磁场中运动时间t的范围．
参考答案：（1）若粒子带负电，且恰好能从d点射出磁场，它运动的轨迹如图1，
则运动的半径：R=L2，
运动的过程洛伦兹力提供向心力，得：qv0B=mv20R
整理得：ν0=BqL2m
（2）若粒子带正电，粒子运动的轨迹如右图所示，当粒子的速度大于与R1相对应的速度v1时，粒子将从dc边射出．
由几何关系可得：R1=L①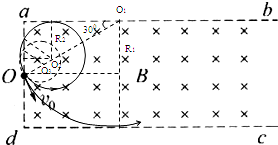
由洛仑兹力和向心力公式可得：qv1B=mv21R1 ②
当粒子的速度小于与R2相对应的速度v2时，粒子将从ad边射出．
由几何关系可得：12L-R2=12R2 ③
由③式解得：R2=13L ④
由洛仑兹力和向心力公式可得：qv2B=mv22R2 ⑤
将①④式分别代入②⑤式可解得：v1=qBLm；v2=qBL3m ⑥
所以v0的取值范围是qBL3m≤v0≤qBLm ⑦
从图中可以看出，当轨迹的半径对应R1时从ab边上射出使用的时间最短，此时对应的圆心角为：
θ=180°-30°=150°
由公式可得：T=2πRv=2πmqB⑧
根据周期与运动时间的关系得：θ360°=t1T
整理得：t1=5πm6qB ⑨
粒子在磁场中运动的时间最长，其做圆周运动的圆心角必然最大，在答图中，当粒子的速度小于v2时，粒子从ad边的不同位置射出时，其半径虽不同，但圆心角的夹角都是300°=56×2π，所以粒子在磁场中的运动时间也是5T6，此即粒子在磁场中运动的最长时间．
所以粒子运动的最长时间为：t2=5T6=5πm3qB⑩
与粒子在磁场中运行时间相对应的t的大小范围是5πm6Bq＜t≤5πm3Bq：
答：（1）ν0=BqL2m（2）v0的取值范围BqL3m≤ν0≤BqLm，粒子在磁场中运动时间t的范围5πm6Bq＜t≤5πm3Bq．
本题解析：
本题难度：简单
2、简答题 如图所示，水平地面上有一辆固定有长为L的竖直光滑绝缘管的小车，管的底部有一质量m=0.2g、电荷量q=8×10-5C的小球，小球的直径比管的内径略小．在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度为B1=15T的匀强磁场，MN面的上方还存在着竖直向上、场强E=25V/m的匀强电场和垂直纸面向外、磁感应强度B2=5T的匀强磁场．现让小车始终保持v=2m/s的速度匀速向右运动，以带电小球刚经过场的边界PQ为计时的起点，测得小球对管侧壁的弹力FN随高度h变化的关系如图所示．g取10m/s2，π取3.14，不计空气阻力．求：
（1）小球刚进入磁场B1时的加速度大小a；
（2）绝缘管的长度L；
（3）小球离开管后再次经过水平面MN时距管口的距离△x．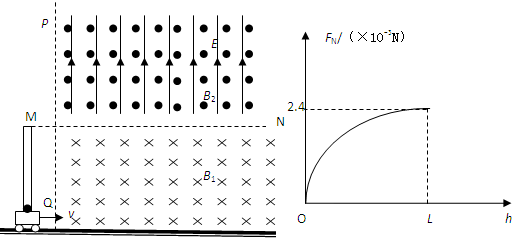
参考答案：（1）以小球为研究对象，竖直方向小球受重力和恒定的洛伦兹力f，故小球在管中竖直方向做匀加速直线运动，加速度设为a，则a=f-mgm=qvB1-mgm=2m/s2
即小球刚进入磁场B1时的加速度大小a为2m/s2．
（2）在小球运动到管口时，FN=2.4×10-3N，设v1为小球竖直分速度，由FN=qv1B1，则v1=FNqB1=2m/s
由v21=2aL得L=v212a=1m
即绝缘管的长度L为1m．
（3）小球离开管口进入复合场，其中qE=2×10-3N，mg=2×10-3N．故电场力与重力平衡，小球在复合场中做匀速圆周运动．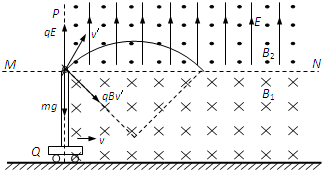
合速度v′=
本题解析：
本题难度：一般
3、选择题 如图所示，在x轴上方存在垂直于纸面向外、磁感应强度为B的匀强磁场．一带电粒子从坐标原点O处以速度v沿y轴正方向进入磁场，最后从P（a，0）射出磁场．不计粒子重力，该带电粒子的电性和比荷
| q m |
| v aB |
| v aB |
| 2v aB |
| 2v aB |
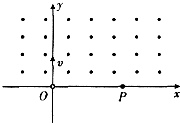
参考答案：由图意可知粒子沿顺时针方向运动，根据左手定则可得粒子带正电
由几何关系得运动半径为：r=a2
由牛顿的定律得：Bqv=mv2r
故有：qm=2vBa
故选C
本题解析：
本题难度：一般
4、计算题 如图，真空室内存在一有右边界的匀强磁场区域，磁感应强度B=0.332T，磁场方向垂直于纸面向里，右边界cd为荧光屏（粒子打上去会发光）。在磁场中距荧光屏d=8cm处有一点状α粒子放射源S，可沿纸面向各个方向均匀放射初速率相同的α粒子，已知：α粒子的质量m=6.64×10－27 kg，电荷量q?=?3.2×10－19 C，初速?度v?=?3.2×106m/s。（可能用到的三角函数：sin37°=?0.6，sin30°=?0.5）求：
（1）α粒子在磁场中作圆周运动的轨道半径R；?
（2）荧光屏cd被α粒子射中而发光的区域长度L；
（3）若从放射源打出的α粒子总个数为3.6×1010个，则最终能打到荧光屏上的α粒子个数为多少？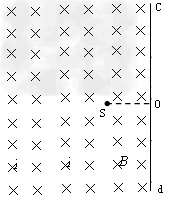 
参考答案：(1)R=20cm=0.2m
(2)o点上方16cm，o点下方16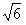
cm，发光长度为：y=16（1+
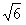）cm
(3)2.54×1010个
本题解析：
本题难度：一般
5、简答题 如图所示，大量质量为m、电荷量为+q的粒子，从静止开始经极板A、B间加速后，沿中心线方向陆续进入平行极板C、D间的偏转电场，飞出偏转电场后进入右侧的有界匀强磁场，最后从磁场左边界飞出．已知A、B间电压为U0；极板C、D长为L，间距为d；磁场的磁感应强度大小为B，方向垂直纸面向里，磁场的左边界与C、D右端相距L，且与中心线垂直．假设所有粒子都能飞出偏转电场，并进入右侧匀强磁场，不计粒子的重力及相互间的作用．则：
（1）求粒子在偏转电场中运动的时间t；
（2）求能使所有粒子均能进入匀强磁场区域的偏转电压的最大值U；
（3）接第（2）问，当偏转电压为
| U 2 |
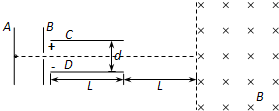
参考答案：（1）粒子在AB间加速，有：
qU0=12mv20-0
又粒子在偏转电场中，水平方向：L=v0t，所以：
t=L
本题解析：
本题难度：一般