时间:2019-03-15 17:39:26
1、简答题 一端开口的钢制圆筒在开口端放一轻活塞，活塞与筒壁摩擦及活塞重均不计，现将开口端向下竖直缓慢地放入7℃时的水中，筒底恰与水面相平时，筒静止。此时筒内气柱长1.4m，当水温升到27℃时，求筒底露出水面多高？(筒壁厚不计)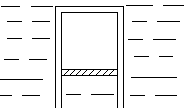
参考答案：
0.1m
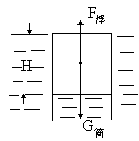
本题解析：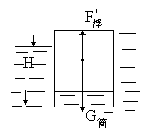
本题难度：简单
2、计算题 如图所示，一端封闭的均匀玻璃管长H＝60cm，开口端竖直向上，用水银封住一定量的空气，水银柱长h＝19 cm，空气柱长L1＝20 cm，初始温度为t1＝27℃。（已知大气压强为76cmHg）求：
（1）初始玻璃管内封闭气体压强p1。
（2）将玻璃管缓缓顺时针转90°，直至玻璃管水平时，空气柱长度L2。
（3）保持玻璃管水平，对气体缓慢加热，则温度至少升高至多少摄氏度时水银全部从管中溢出。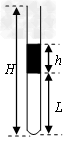
参考答案：解：（1）p1＝（76＋19）cmHg＝95cmHg?
（2）等温过程p1V1＝p2V2?
95×20＝76×L2
L2＝25cm
（3）等压过程V2/T2＝V3/T3
25/300＝60/T3
T3＝720K?
t3＝447°C
本题解析：
本题难度：一般
3、选择题 民间常用“拔火罐”来治疗某些疾病，方法是将点燃的纸片放入一个小罐内，当纸片燃烧完时，迅速将火罐开口端紧压在皮肤上，火罐就会紧紧地被“吸”在皮肤上。其原因是，当火罐内的气体
A．温度不变时，体积减小，压强增大
B．体积不变时，温度降低，压强减小
C．压强不变时，温度降低，体积减小
D．质量不变时，压强增大，体积减小
参考答案：B
本题解析：把罐扣在皮肤上，罐内空气的体积等于火罐的容积，体积不变，气体经过热传递，温度不断降低，气体发生等容变化，由查理定律可知，气体压强减小，火罐内气体压强小于外界大气压，大气压就将罐紧紧地压在皮肤上．故选B．
考点：查理定律。
本题难度：一般
4、计算题 如图所示，两个可导热的气缸竖直放置，它们的底部都由一细管连通（忽略细管的容积）。两气缸各有一个活塞，质量分别为m1和m2，活塞与气缸无摩擦。活塞的下方为理想气体，上方为真空。当气体处于平衡状态时，两活塞位于同一高度h。（已知m1＝3m，m2＝2m）
（1）在两活塞上同时各放一质量为m的物块，求气体再次达到平衡后两活塞的高度差（假定环境温度始终保持为T0）。
（2）在达到上一问的终态后，环境温度由T0缓慢上升到T，试问在这个过程中，气体对活塞做了多少功？气体是吸收还是放出了热量？（假定在气体状态变化过程中，两物块均不会碰到气缸顶部）。 
参考答案：解：（1）设左、右活塞的面积分别为A"和A，由于气体处于平衡状态，故两活塞对气体的压强相等，即：
由此得：
在两个活塞上各加一质量为m的物块后，右活塞降至气缸底部，所有气体都在左气缸中
在初态，气体的压强为
，体积为
；在末态，气体压强为
，体积为
（x为左活塞的高度）
由玻意耳－马略特定律得：
解得：
，即两活塞的高度差为
（2）当温度由T0上升至T时，气体的压强始终为
，设x"是温度达到T时左活塞的高度，由盖·吕萨克定律得：
活塞对气体做的功为：
由热力学第一定律：
，W<0，ΔU>0，∴Q>0，在此过程中气体吸收热量
本题解析：
本题难度：一般
5、计算题 （10分）如图所示，在长为L=57cm的一端封闭、另一端开口向上的竖直玻璃管内，用4cm高的水银柱封闭着51cm长的理想气体，管内外气体的温度均为33℃ ，大气压强p0=76cmHg.
①若缓慢对玻璃管加热，当水银柱上表面与管口刚好相平时，求管中气体的温度；
②若保持管内温度始终为33℃，现将水银缓慢注入管中，直到水银柱上表面与管口相平，求此时管中气体的压强。
参考答案：（1）T2=318K （2）P2=85cmHg
本题解析：①设玻璃管横截面积为S，以管内封闭气体为研究对象， 气体经等压膨胀：
初状态：
末状态：
（1分）
由盖—吕萨克定律：
（2分） 得T2=318K （1分）
②当水银柱上表面与管口相平，设此时管中气体压强为P，水银柱的高度为H，管内气体经等温压缩：
初状态：V1=51S P1= 80cmHg （1分）
末状态：
（1分）
由玻意耳定律：
（2分）
得 H=9cm（1分）
故P2=85cmHg（1分）
考点：本题考查盖—吕萨克定律和玻意耳定律。
本题难度：一般