时间:2019-03-15 17:27:57
1、选择题 一辆公共汽车进站后开始刹车，做匀减速直线运动。开始刹车后的第1s内和第2s内的位移大小依次为11m和9m。则刹车后7s内的位移是
A．24m
B．35m
C．36m
D．49m
参考答案：C
本题解析：汽车的加速度为：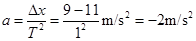
，根据
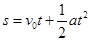，则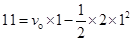
，解得：v0="12m/s" ,故物体停止的时间：
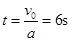，刹车后7s内的位移是6s内的位移
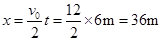，选项C正确。
考点：匀变速运动的规律.
本题难度：一般
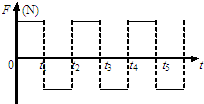
2、选择题 一个物体受到的合力F如图所示，该力的大小不变，方向随时间t周期性变化，力为正时表示力的方向向东，力为负时表示力的方向向西，力的总作用时间足够长，将物体在下面哪些时刻由静止释放，物体可以运动到出发点的西边且离出发点很远的地方（ ）
A．t=t1
B．t=
| t1 2 |
| 2t1 3 |
| t1 3 |
参考答案：
A、物体在t1时刻由静止释放，将先向西做匀加速直线运动，再向西做匀减速直线运动…这样一直向西运动，能到达出发点的西边且离出发点很远的地方．故A正确．
B、物体在t12时刻由静止释放，将先向东做匀加速直线运动，再向东做匀减速直线运动，速度减为零后向西做匀加速直线运动，再向西做匀减速运动，经过一个周期时速度减为零，物体做往往复运动，不能到达出发点的西边且离出发点很远的地方．故B错误．
C、物体在23t1时刻由静止释放，将先向东做匀加速直线运动，再向东做匀减速直线运动，速度减为零后向西做匀加速直线运动，再向西做匀减速运动，由于向西运动的时间长，而加速度大小不变，向西运动的位移总大于向东的位移，则物体可以运动到出发点的西边且离出发点很远的地方．故C正确．
D、物体在t13时刻由静止释放，将先向东做匀加速直线运动，再向东做匀减速直线运动，速度减为零后向西做匀加速直线运动，再向西做匀减速运动，由于向东运动的时间长，而加速度大小不变，向东运动的位移总大于向西的位移，则物体运动到出发点的东边且离出发点很远的地方．故D错误．
故选AC
本题解析：
本题难度：一般
3、简答题 某一物体以v速度在粗糙水平面上作匀变速直线运动，从某一时刻开始计时测得第三秒末和第七秒末的速度分别为3米/秒和2米/秒，求：
（1）物体运动的加速度大小；
（2）开始计时时物体运动的速度；
（3）开始计时后20秒内通过的位移．
参考答案：（1）物体运动的加速度? a=v7-v3△t=2-34m/s2=-0.25m/s2
则加速度大小为0.25m/s2．
（2）由v3=v0+at得
v0=v3-at=3+0.25×3（m/s）=3.75m/s
（3）设物体从开始计时到停止运动所用的时间为t停．
则t停=0-v0a=0-3.75-0.25=15s＜20s
故20s时车已停下，则开始计时后20秒内通过的位移为
? s=12v0t停=28.125m
答：
（1）物体运动的加速度大小为0.25m/s2．
（2）开始计时时物体运动的速度为3.75m/s；
（3）开始计时后20秒内通过的位移为28.125m．
本题解析：
本题难度：一般
4、选择题 一个物体在水平面上以恒定加速度运动，它的位移与时间的关系x=24t-6t2，则它的速度为零的时刻是（ ）
A．
| 1 6 |
参考答案：根据x=v0t+12at2=24t-6t2得，初速度v0=24m/s，加速度a=-12m/s2，
根据速度时间公式得，v=v0+at
解得t=0-v0a=0-24-12=2s．故B正确，A、C、D错误．
故选：B．
本题解析：
本题难度：一般
5、计算题 （15分）交管部门强行推出了“电子眼”，机动车违规现象大幅度减少．现有甲、乙两汽车正沿同一平直马路同向匀速行驶，甲车在前，乙车在后，行驶速度v0均为54km/h．当两车快要到十字路口时，甲车司机看到红灯亮起，于是紧急刹车，乙车司机看到甲车刹车后也紧急刹车（乙车司机的反应时间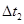
=0.4s，反应时间内视为匀速运动）．已知甲车、乙车紧急刹车时产生的加速度大小分别为
、
．
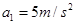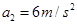（1）若甲 司机看到红灯时车头距警戒线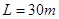
，要避免闯红灯，他的反应时间
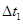不能超过多少？
（2）乙车刹车后经多长时间速度与甲车相等？
（3）为保证两车在紧急刹车过程中不相撞，甲、乙两车刹车前的距离x0至少多大？
参考答案：⑴Δt1＝0.5s；⑵t＝2s；⑶x0＝2.4m。
本题解析：⑴甲车在司机反应时间内前进的距离为：x11＝v0Δt1?①
刹车后至停止前进的距离为：x1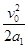2＝
?②
要使甲车避免闯红灯需要满足的条件为：x11＋x12≤L?③
由①②③式联立并代入数据解得：Δt1≤0.5s，即要使甲车避免闯红灯司机的反应时间Δt1不能超过0.5s。
⑵设甲乙两车刹车后分别经过时间t1、t2速度减小为零，根据匀变速直线运动规律有：
t1＝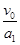
＝3s，t2＝
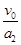＝2.5s
不妨假设乙车刹车后经过时间t后，速度与甲车相等，根据匀变速直线运动速度公式有：
v0－a1(t＋Δt2)＝v0－a2t，代入数据解得：t＝2s
显然t＜t1，t＜t2，即两车还未停止运动，t＝2s符合题意。
⑶当甲刹车后，两车间的距离逐渐减小，若从两车都刹车时起，至两车速度相等时止，两车不能相撞，则往后两车不可能相撞，由第⑵问的求解可知，甲车刹车运动的时间为(t＋Δt2)，根据匀变速直线运动位移公式有：甲车的位移为：x1＝v0(t＋Δt2)－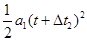
?④
乙车的位移为：x2＝v0Δt2＋v0t－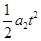
?⑤
要使两车不相撞应满足：x2－x1≤x0?⑥
由④⑤⑥式联立并代入数据解得：x0≥2.4m
即为保证两车不相撞，甲、乙两车刹车前的距离x0至少2.4m。
本题难度：一般