时间:2019-03-15 17:22:41
1、计算题 如图所示,光滑水平面MN的左端M处有一弹射装置P(P为左端固定,处于压缩状态且锁定的轻质弹簧,当A与P碰撞时P立即解除锁定),右端N处与水平传送带恰平齐且很靠近,传送带沿逆时针方向以恒定速率υ =" 5m/s" 匀速转动,水平部分长度L = 4m。放在水平面上的两相同小物块A、B(均视为质点)间有一被压缩的轻质弹簧,弹性势能Ep = 4J,弹簧与A相连接,与B不连接,A、B与传送带间的动摩擦因数μ = 0.2,物块质量mA = mB = 1kg。现将A、B由静止开始释放,弹簧弹开,在B离开弹簧时,A未与P碰撞,B未滑上传送带。取g = 10m/s2。求:
(1)B滑上传送带后,向右运动的最远处与N点间的距离sm;
(2)B从滑上传送带到返回到N端的时间t和这一过程中B与传送带间因摩擦而产生的热?能Q;
(3)B回到水平面后压缩被弹射装置P弹回的A上的弹簧,B与弹簧分离然后再滑上传?送带。则P锁定时具有的弹性势能E满足什么条件,才能使B与弹簧分离后不再与弹簧相碰。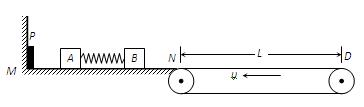
参考答案:(1)弹簧弹开的过程中,系统机械能守恒
Ep = mAυA2 + mBυB2?(1分)
由动量守恒有? mAυA- mBυB =" 0?" (1分)
联立以上两式解得? υA =" 2m/s?" υB =" 2m/s?" (1分)
B滑上传送带做匀减速运动,当速度减为零时,向右运动的距离最大。
由动能定理得?- μmBgsm = 0- mBυB2?(1分)
解得? sm = =" 1m?" (1分)
(2)物块B先向右做匀减速运动,直到速度减小到零,然后反方向做匀加速运动,?回到皮带左端时速度大小仍为υB = 2m/s?(1分)
由动量定理? - μmBgt =" -" mBυB - mBυB?(1分)
解得? t = =" 2s?" (1分)
B向右匀减速运动因摩擦而产生的热能为
Q1 = μmBg(υ·+ sm)?(1分)
B向左匀加速运动因摩擦而产生的热能为
Q2 = μmBg(υ·- sm)?(1分)
Q = Q1 + Q2 = μmBgυt = 20J?(1分)
(3)设弹射装置P将A弹开时的速度为υA′,则
E = mAυA′2- mAυA2?(2分)
B离开弹簧时,AB速度互换,B的速度? υB′ = υA′?(2分)
B与弹簧分离后不再与弹簧相碰,则B滑出平台Q端,由能量关系有
mBυB′2 > μmBgL?(2分)
以上三式解得
E > μmAgL- mAυA2?(2分)
代入数据解得? E> 6J?(1分)
本题解析:略
本题难度:一般
2、简答题 电场中有a、b两点,将一个带电量为2×10-8C的正电荷从a点移到b点,电场力做功-4×10-6J,求:a、b两点的电势差.若将带电量为8×10-7C的负电荷从a移到b,电场力做功为多少?
参考答案:a、b两点的电势差Uab=Wabq=-4×10-62×10-8V=-200V
a、b两点的电势差与试探电荷无关,是定值,故将带电量为8×10-7C的负电荷从a移到b,电场力做功为
? Wab′=q′Uab=-8×10-7×(-200)J=1.6×10-4J
答:a、b两点的电势差为-200V.若将带电量为8×10-7C的负电荷从a移到b,电场力做功为1.6×10-4J.
本题解析:
本题难度:一般
3、选择题 如图所示,闭合的矩形金属框以一定的初速度v沿足够大的光滑(不计一切摩擦性阻力包括空气阻力)的绝缘水平面向右运动,进入有界的匀强磁场区域,如果金属框会停止运动,它停止运动的位置只可能是图中的( )
A.ac
B.bd
C.cd
D.abc
参考答案:线框进入磁场的过程中,磁通量增加,产生感应电流,线框受到安培力而做减速运动,则在a位置时线框可能停止运动;
线框完全进入磁场的过程中,磁通量不变,不产生感应电流,线框不受安培力而做匀速运动,则在b位置线框不可能停止运动;
线框穿出磁场的过程中,磁通量减小,产生感应电流,线框受到安培力而做减速运动,则在c位置时线框可能停止运动;
线框完全穿出磁场的过程中,不产生感应电流,线框做匀速运动,则在d位置线框不可能停止运动;
故选A
本题解析:
本题难度:一般
4、填空题 用如图所示的装置,探究功与物体速度变化的关系.实验时,先适当垫高木板,然后由静止释放小车,小车在橡皮条弹力的作用下被弹出,沿木板滑行.小车滑行过程中带动通过打点计器的纸带,记录共运动情况.观察发现纸带前面部分点迹疏密不匀,后面部分点迹比较均匀,回答下列问题:
(1)适当垫高木板是为了______;
(2)通过纸带求小车速度时,应使用纸带的______(填“全部”、“前面部分”或“后面部分”);
(3)若实验作了n次,所用橡皮条分别为1根、2根…n根,通过纸带求出小车的速度分别为v1、v2…vn,用W表示橡皮条对小车所做的功,作出的W-v2图线是一条过坐标原点的直线,这说明W与v的关系是______.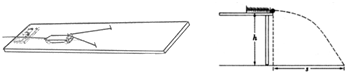
参考答案:(1)用 1 条、2 条、3 条 …同样的橡皮筋将小车拉到同一位置释放,橡皮筋拉力对小车所做的功依次为 w、2w、3w …探究橡皮筋拉力对小车所做的功W与小车速度v的定量关系.将木板放有打点计时器的一端垫高,小车不连橡皮筋,尾部固定一纸带,轻推小车使小车沿木板向下运动,如果纸带上打出的点间距是均匀的,说明纸带的运动是匀速直线运动,小车重力沿斜面方向的分力刚好平衡了小车所受的摩擦力.
(2)橡皮筋拉力对小车所做的功全部完成后,打出来的点才能反映物体的速度.所以应使用纸带的后面部分.
(3)W-v2图线是一条过坐标原点的直线,根据数学知识可确定W与速度v的平方成正比.
答:(1)平衡摩擦力(2)后面部分(3)W与速度v的平方成正
本题解析:
本题难度:一般
5、简答题 如图,长木板ab的b端固定一挡板,木板连同挡板的质量为M=4.0kg,a、b间距离s=2.0m.木板位于光滑水平面上.在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数μ=0.10,它们都处于静止状态.现令小物块以初速v0=4.0m/s,沿木板向前滑动,直到和挡板相碰.碰撞后,小物块恰好回到a端而不脱离木板.求碰撞过程中损失的机械能.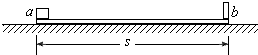
参考答案:设木板和物块最后共同运动的速度为v,由动量守恒定律mv0=(m+M)v-----①
设全过程损失的机械能为E,E=12mv20-12(m+M)v2------------②
用W表示在全过程中摩擦力做的总功,则W=-2μmgs----------③
用E1表示在碰撞过程中损失的机械能,则E1=E-W-------④
由以上各式解得E=12mMm+mv20-2μmgs-----------⑤
代入数据解锝
E1=2.4J?
碰撞过程中损失的机械能为2.4J.
本题解析:
本题难度:一般