时间:2019-03-15 17:14:36
1、简答题 两根光滑的长直金属导轨M?N、M′N′平行置于同一水平面内,导轨间距为l,电阻不计,M、M′处接有如图所示的电路,电路中各电阻的阻值均为R,电容器的电容为C.长度也为l、阻值同为R的金属棒a?b垂直于导轨放置,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中.a?b在外力作用下向右匀速运动且与导轨保持良好接触,在ab运动距离为s的过程中,整个回路中产生的焦耳热为Q.求
(1)a?b运动速度v的大小;
(2)电容器所带的电荷量q.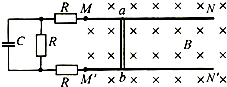
参考答案:(1)设a?b上产生的感应电动势为E,回路中的电流为I,a?b运动距离s所用时间为t,则有:
E=Blv? ?①
I=E4R? ?②
t=sv? ?③
Q=I2(4R)t? ④
由上述方程得:v=4QRB2l2s
故a?b运动速度v的大小为:v=4QRB2l2s
(2)设电容器两极板间的电势差为U,则有:U=IR? ⑤
电容器所带电荷量:q=CU? ⑥
解得:q=CQRBls
故电容器所带的电荷量为:q=CQRBls.
本题解析:
本题难度:一般
2、计算题 亮亮星期天跟妈妈去商厦购物,亮亮做了一个有趣的实验。他发现,乘自动扶梯上楼,如果站在扶梯上不动,扶梯可以在60s内把他送到楼上去.若扶梯不动,他可用 30s沿扶梯走到楼上.试计算亮亮在仍以原来的速度沿扶梯向上运动,同时扶梯也开动的情况下,需用多长时间才能到楼上?
参考答案:
本题解析:设沿着扶梯从楼下到楼上的距离为x,扶梯的运动速度为v1,亮亮的速度为v2,站在扶梯上不动,扶梯把他送到楼上去的时间为t1,扶梯不动,他沿扶梯走到楼上去的时间为t2,则有
x=v1t1? x=v2t2
亮亮和扶梯同时运动时,x=(v1+v2)t
解以上三式得? t=20s
所以,亮亮以原来的速度沿扶梯向上运动,同时扶梯也开动的情况下,需用20s 时间才能到楼上
点评:已知自动扶梯把站在上面不动的人送到楼上所用时间和人自己走上去所用时间,楼高度不变,可求人沿着开动的扶梯走上去所需的时间.
本题难度:一般
3、计算题 一列火车长160米,通过长440米的桥用了30秒,问火车速度是多少?
参考答案:v=20(m/s)
本题解析:此题是一道典型的过桥问题,在车长、桥长、车速和过桥时间4个物理量中,给了三个,求另外一个。过桥问题首先要解决的是车通过的路程为车长+桥长。然后把路程用公式展开,得到过桥的通用字母式。此题求的是火车速度v。
本题难度:简单
4、选择题 一辆汽车以20m/s的速度作匀速直线运动,从某时刻开始汽车紧急刹车,刹车后的加速度大小为4.0m/s2,则从刹车起,汽车在6.0秒末的速度大小是
A.0m/s
B.2.0m/s
C.2.4m/s
D.4.0m/s
参考答案:A
本题解析:分析:根据匀变速直线运动速度时间公式求出汽车刹车到停止所需的时间,判断汽车是否停止,因为汽车速度为零后不再运动.
解答:根据匀变速直线运动的时间公式得,汽车刹车到停止所需的时间t0=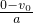 =
=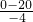 s=5s<6s.知6s末速度为零.故A正确,B、C、D错误.
s=5s<6s.知6s末速度为零.故A正确,B、C、D错误.
故选A.
点评:解决本题的关键掌握匀变速直线运动运动学公式,并能灵活运用.注意该问题属于“刹车”问题.
本题难度:一般
5、计算题 甲、乙两人从在一条直线上相距1000m的两地同时相向匀速直线而行,甲的速度是3.0m/s,乙的速度是2.0m/s,两人相遇时刻起,要想同时到达对方原来的出发点,哪个人应该增大运动速度?增大的运动速度应为多大?
参考答案:解:乙的速度应增加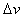 ?
?
? 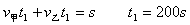
? 甲、乙走完全程的时间为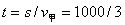 ?
?
? 对乙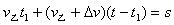
?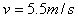
本题解析:
本题难度:一般