时间:2019-03-15 16:57:47
1、计算题 （9分）普朗克常量h＝6.63×10－34 J·s，铝的逸出功W0＝6.72×10－19 J，现用波长λ＝200 nm的光照射铝的表面（结果保留三位有效数字）．
①求光电子的最大初动能；
②若射出的一个具有最大初动能的光电子正对一个距离足够远且静止的电子运动，求在此运动过程中两电子电势能增加的最大值（除两电子间的相互作用以外的力均不计）。
参考答案：（1）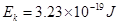
?（2）1.62×10-19J
本题解析：（1）由
?和 
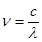?得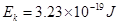
（2）增加的电势能来自系统损失的动能，当两电子的速度相等时电势能最大，由动量守恒定律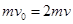 
?和?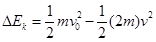
?
得：
所以增加的电势能最大值为1.62×10-19J
本题难度：一般
2、选择题 一个γ光子的能量为E，动量为P，射到一个静止的电子上，被电子反射回来，其动量大小变为P1，能量变为E1，电子获得的动量为P2，动能为E2则有
A．E1
参考答案：
本题解析：
本题难度：一般
3、选择题 沿着一条光滑的水平导轨放一个条形磁铁，质量为M，它的正前方隔一定距离的导轨上再放质量为m的铝块．给铝块某一初速度v使它向磁铁运动，下述说法中正确的是（导轨很长，只考虑在导轨上的情况）（ ）
A．磁铁将与铝块同方向运动
B．铝块的速度减到
| mv m+M |
| 1 2 |
参考答案：A、根据楞次定律的表现：“来拒去留”，所以铝制成的滑块向磁铁滑去时，滑块中产生的感应电流对磁铁是“拒”的作用，即阻碍作用，阻碍磁铁的靠近，也可理解为滑块和磁铁之间为排斥力，则铝块减速，磁铁加速，运动方向与铝块同方向，A正确；
B、二者最后达到一相同速度，设铝块速度方向为正，根据动量守恒定律：mv=（M+m）v′，得：v′=mvm+M，B正确D错误；
C、铝块和磁铁最后总动能为：12（M+m）v′2=12m2v2M+m，故C错误；
故选：AB．
本题解析：
本题难度：简单
4、简答题 质量分别为3m和m的两个物体，用一根细线相连，中间夹着一个被压缩的轻质弹簧，整个系统原来在光滑水平地面上以速度V0向右匀速运动，如图所示。后来细线断裂，质量为m的物体离开弹簧时的速度变为2V0。求
（1）质量为3m的物体最终的速度；
（2）绳断前弹簧的弹性势能。
参考答案：
（1）
（2）
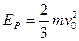
本题解析：设3m的物体离开弹簧时的速度为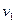
，由动量守恒定律得：
?(4分)?
所以??(3分)
由能量守恒定律得：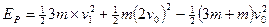
?(4分)
所以弹性势能?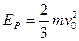?(3分)
本题难度：简单
5、选择题 一颗子弹水平射入置于光滑水平面上的木块A并留在其中，A、B用一根弹性良好的轻质弹簧连在一起，如图所示．则在子弹打击
木块A及弹簧被压缩的过程中，对子弹、两木块和弹簧组成的系统
[? ]
A．动量守恒，机械能守恒
B．动量不守恒，机械能守恒
C．动量守恒，机械能不守恒
D．无法判定动量、机械能是否守恒
参考答案：C
本题解析：
本题难度：简单