时间:2018-10-13 01:45:04
1、计算题 (10分)在边长为a的等边三角形ABC区域内有一匀强磁场,磁感应强度为B,方向垂直纸面向里,一带正电的粒子质量为m,电量为q,由BC边中点O沿平行于AB的方向射入磁场,速度大小为v0,忽略粒子的重力.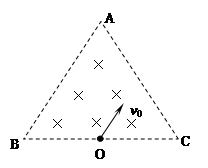
(1)若粒子刚好垂直AB边飞出磁场,求粒子在磁场中的运动时间;
(2)如果要求粒子在磁场中的飞行时间最长,求粒子的速度必须满足的条件。
参考答案:(1)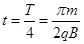 (2)
(2)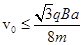
本题解析:(1)粒子仅在洛仑兹力作用下在磁场内做匀速圆周运动,如刚好垂直AB边飞出,其运动轨迹如图所示,其中O1为圆心位置,O1O为半径R.洛仑兹力充当向心力,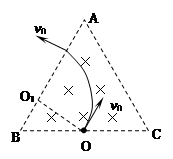
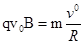 ?①
?①
周期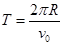 ?②
?②
解得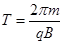 ?③
?③
粒子在场中的运动时间为t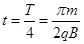 ?④
?④
(2)粒子在磁场中的飞行时间最长,须使粒子从BC边飞出.如刚好使粒子从BC边飞出其运动轨迹恰与AB边相切,如图所示,其中O2为圆心位置,O2O为半径R0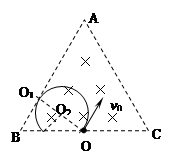
其中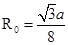 ?⑤
?⑤
粒子从BC边飞出,半径R≤R0?⑥
由①式解得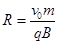 ?⑦
?⑦
由⑤⑥⑦式可得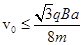 ?⑧
?⑧
点评:此类题型考察了带电粒子在磁场中的运动。通常这类问题都会涉及到轨迹问题,所以一般解题思路为:定圆心、找半径,画轨迹
本题难度:一般
2、选择题 如图所示,水平桌面处在竖直向下的匀强磁场中,桌面上平放着一只内壁光滑的玻璃试管,管的底部M处有一带电小球.在水平拉力F作用下,试管向右做匀速运动时,小球向管口N运动,则( )
A.小球带负电
B.小球带正电
C.在小球未从管口出去前,拉力F逐渐变大
D.在小球未从管口出去前,拉力F保持不变
参考答案:A、小球能从管口处飞出,说明小球受到指向管口洛伦兹力,根据左手定则判断,小球带正电.故A错误,B正确;
C、设管子运动速度为v1,小球沿管子的分速度大小为v2,则小球受到垂直管子向左的洛伦兹力的分力F2=qv2B,v2增大,则F2增大,而拉力F=F2,则F逐渐增大.故C正确,D错误.
故选:BC
本题解析:
本题难度:一般
3、计算题 (16分)如图所示,NM的上侧有匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小为B。一带负电的粒子(不计重力)从P处以垂直于MN的初速度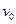 射入磁场区域,最后通过
射入磁场区域,最后通过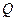 点。已知此粒子的比荷
点。已知此粒子的比荷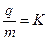 ,求:
,求:
(1)P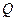 间的距离L?
间的距离L?
(2)粒子从P运动到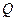 需要多长的时间?
需要多长的时间?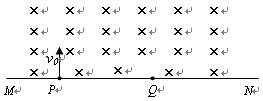
参考答案:(1)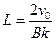
(2)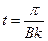
本题解析:(1)L=2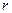 …………(2分)
…………(2分)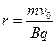 ?…………(4分)
?…………(4分)
得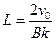 …………(2分)
…………(2分)
(2)粒子从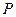 到
到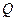 运动的时间
运动的时间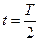 …………(2分)
…………(2分)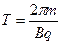 ………(4分)
………(4分)
得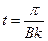 ………(2分)
………(2分)
本题难度:简单
4、计算题 图中左边有一对平行金属板,两板相距为d,电压为u,两板之间有匀强磁场,磁场应强度大小为B0,方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面,垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力
(1)已知这些离子中的离子甲到达磁场边界EG后,从边界EF穿出磁场,求离子甲的质量。
(2)已知这些离子中的离子乙从EG边上的I点(图中未画出)穿出磁场,且GI长为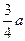 ,求离子乙的质量。
,求离子乙的质量。
(3)若这些离子中的最轻离子的质量等于离子甲质量的一半,而离子乙的质量是最大的,问磁场边界上什么区域内可能有离子到达。
参考答案:1)由题意知,所有离子在平行金属板之间做匀速直线运动,它所受到的向上的磁场力和向下的电场力平衡,有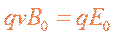 ?①
?①
式中
,v是离子运动的速度,E0是平行金属板之间的匀强电场的强度,有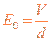 ?②
?②
由①②式得: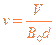
③
在正三角形磁场区域,离子甲做匀速圆周运动。设离子甲质量为m,
由洛仑兹力公式和牛顿第二定律有: 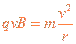 ?④
?④
式中,r是离子甲做圆周运动的半径。离子甲在磁场中的运动轨迹为半圆,圆心为O:这半圆刚好与EG边相切于K,与EF边交于I/点。在ΔEOK中,OK垂直于EG。
由几何关系得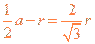 ?⑤
?⑤
由⑤式得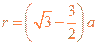 ?⑥
?⑥
联立③④⑥式得,离子甲的质量为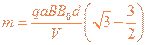 ?⑦
?⑦
(2)同理,有洛仑兹力公式和牛顿第二定律有?⑧
式中,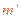 和
和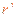 分别为离子乙的质量和做圆周运动的轨道半径。离子乙运动的圆周的圆心
分别为离子乙的质量和做圆周运动的轨道半径。离子乙运动的圆周的圆心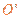 必在E、H两
必在E、H两 点之间,又几何关系有
点之间,又几何关系有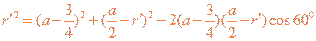
⑨
由⑨式得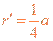 ⑩
⑩
联立③⑧⑩式得,离子乙的质量为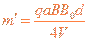 ?⑾
?⑾
(3)对于最轻的离子,其质量为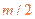 ,由④式知,它在磁场中做半径为
,由④式知,它在磁场中做半径为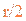 的匀速圆周运动。因而与EH的交点为O,有
的匀速圆周运动。因而与EH的交点为O,有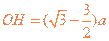 ⑿
⑿
当这些离子中的离子质量逐渐增大到m时,离子到达磁场边界 上的点的位置从
上的点的位置从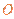 点沿
点沿 边变到
边变到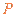 点;当离子质量继续增大时,离子到达磁场边界上的点的位置从
点;当离子质量继续增大时,离子到达磁场边界上的点的位置从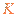 点沿
点沿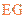 边趋向于
边趋向于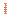 点。
点。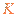 点到
点到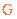 点的距离为
点的距离为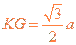 ⒀
⒀
本题解析:略
本题难度:简单
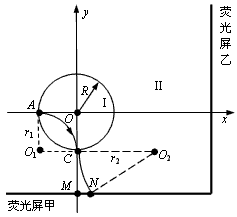
5、计算题 如图所示,圆心在原点、半径为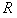 的圆将
的圆将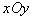 平面分为两个区域,在圆内区域Ⅰ(
平面分为两个区域,在圆内区域Ⅰ(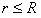 )和圆外区域Ⅱ(
)和圆外区域Ⅱ(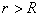 )分别存在两个匀强磁场,方向均垂直于
)分别存在两个匀强磁场,方向均垂直于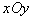 平面。垂直于
平面。垂直于 平面放置两块平面荧光屏,其中荧光屏甲平行于
平面放置两块平面荧光屏,其中荧光屏甲平行于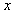 轴放置在
轴放置在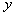 =
=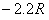 的位置,荧光屏乙平行于
的位置,荧光屏乙平行于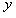 轴放置在
轴放置在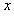 =
=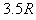 的位置。现有一束质量为
的位置。现有一束质量为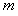 、电荷量为
、电荷量为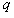 (
(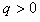 )、动能为
)、动能为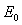 的粒子从坐标为(
的粒子从坐标为(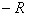 ,0)的
,0)的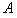 点沿
点沿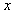 轴正方向射入区域Ⅰ,最终打在荧光屏甲上,出现亮点
轴正方向射入区域Ⅰ,最终打在荧光屏甲上,出现亮点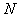 的坐标为(
的坐标为(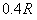 ,
,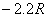 )。若撤去圆外磁场,粒子也打在荧光屏甲上,出现亮点
)。若撤去圆外磁场,粒子也打在荧光屏甲上,出现亮点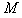 的坐标为(0,
的坐标为(0,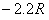 ),此时,若将荧光屏甲沿
),此时,若将荧光屏甲沿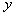 轴负方向平移,发现亮点的
轴负方向平移,发现亮点的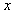 轴坐标始终保持不变。不计粒子重力影响。
轴坐标始终保持不变。不计粒子重力影响。
(1)求在区域Ⅰ和Ⅱ中粒子运动速度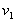 、
、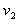 的大小;
的大小;
(2)求在区域Ⅰ和Ⅱ中磁感应强度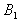 、
、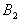 的大小和方向;
的大小和方向;
(3)若上述两个磁场保持不变,荧光屏仍在初始位置,但从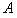 点沿
点沿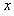 轴正方向射入区域Ⅰ的粒子束改为质量为
轴正方向射入区域Ⅰ的粒子束改为质量为 、电荷量为
、电荷量为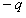 、动能为
、动能为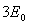 的粒子,求荧光屏上出现亮点的坐标。
的粒子,求荧光屏上出现亮点的坐标。 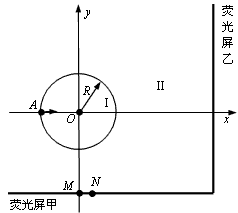
参考答案:解:(1)由于在磁场中运动时洛仑兹力不做功,所以在区域Ⅰ和Ⅱ中粒子运动速度大小就是在 点入射时初始速度大小
点入射时初始速度大小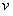 ,由
,由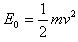 可得
可得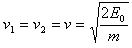 ?
?
(2)粒子在区域Ⅰ中运动了四分之一圆周后,从C点沿 轴负方向进入区域Ⅱ的磁场。如图所示,圆周运动的圆心是
轴负方向进入区域Ⅱ的磁场。如图所示,圆周运动的圆心是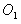 点,半径为
点,半径为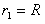
 由
由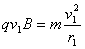 ,得
,得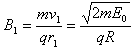 ,方向垂直
,方向垂直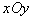 平面向外
平面向外
粒子进入区域Ⅱ后做半径为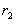 的圆周运动,由
的圆周运动,由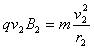 ,可得
,可得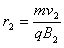
圆周运动的圆心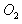 坐标为(
坐标为(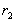 ,
,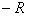 )
)
圆周运动轨迹方程为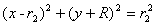
将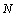 点的坐标(
点的坐标(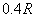 ,
,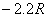 )代入上式,可得
)代入上式,可得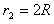
求得: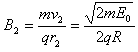 ,方向垂直
,方向垂直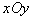 平面向里
平面向里
(3)如图所示,粒子先在区域Ⅰ中做圆周运动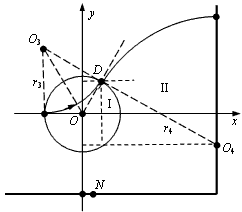 由
由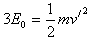 可知,运动速度为
可知,运动速度为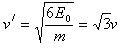
轨道半径为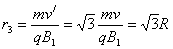
由圆心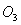 的坐标(
的坐标(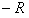 ,
,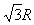 )可知,
)可知,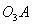 与
与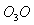 的夹角为
的夹角为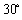 。通过分析如图的几何关系,粒子从D点穿出区域Ⅰ的速度方向与
。通过分析如图的几何关系,粒子从D点穿出区域Ⅰ的速度方向与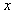 轴正方向的夹角为
轴正方向的夹角为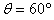
粒子进入区域Ⅱ后做圆周运动的半径为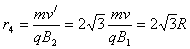
其圆心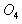 的坐标为(
的坐标为(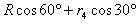 ,
,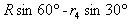 ),即(
),即(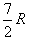 ,
,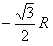 ),说明圆心
),说明圆心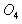 恰好在荧光屏乙上,所以,亮点将出现在荧光屏乙上的P点
恰好在荧光屏乙上,所以,亮点将出现在荧光屏乙上的P点
其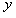 轴坐标为
轴坐标为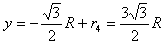
其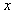 轴坐标为
轴坐标为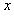 =
=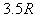
本题解析:
本题难度:困难