时间:2018-10-13 01:04:26
1、计算题 如图所示，半径R＝0.4m的光滑半圆轨道与粗糙的水平面相切于A点，质量为m＝1kg的小物体（可视为质点）在水平拉力F的作用下，从静止开始由C点运动到A点，物体从A点进入半圆轨道的同时撤去外力F，物体沿半圆轨道通过最高点B后做平抛运动，正好落在C点，已知xAC＝2m，F＝15N，g取10m/s2，试求：
（1）物体在B点时的速度大小以及此时半圆轨道对物体的弹力大小；
（2）物体从C到A的过程中，摩擦力做的功。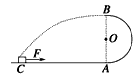 
参考答案：解：（1）设物体在B点的速度为v，由B到C做平抛运动，
有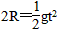
，xAC＝vt，∴v＝5 m/s
由此时受力知
， ∴FN＝52.5 N。
由牛顿第三定律知，半圆轨道对物体的弹力FN′＝52.5 N。
（2）A到B，机械能守恒
由C到A应用动能定理可知
所以，Wf＝－Ff·xAC＝－9.5 J。
本题解析：
本题难度：一般
2、简答题 如图所示，在圆柱形屋顶中心天花板O点，挂一根L="3" m的细绳，绳的下端挂一个质量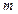
为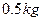
的小球，已知绳能承受的最大拉力为10 N。小球在水平面内做圆周运动，当速度逐渐增大到绳断裂后，小球以
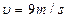的速度落在墙边。求这个圆柱形房屋的高度
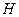和半径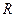
。（g取10 m/s2）?
参考答案：4.8m
本题解析：设绳与竖直方向夹角为θ，则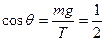
，所以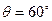
，
小球在绳断时离地高度为：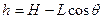
?
小球做匀速圆周运动的半径为：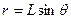
?
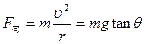
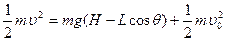
联立①②③④式求得：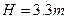
，平抛运动时间为：
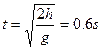，水平距离为：
，
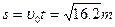圆柱半径为：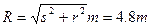
本题难度：一般
3、简答题 电子扩束装置由电子加速器、偏转电场和偏转磁场组成．偏转电场由加有电压的相距为d的两块水平平行放置的导体板组成，匀强磁场的左边界与偏转电场的右边界相距为s，如图甲所示．大量电子（其重力不计）由静止开始，经加速电场加速后，连续不断地沿平行板的方向从两板正中间射入偏转电场．当两板没有加电压时，这些电子通过两板之间的时间为2t0，当在两板间加如图乙所示的周期为2t0、幅值恒为U0的电压时，所有电子均从两板间通过，进入水平宽度为l，竖直宽度足够大的匀强磁场中，最后通过匀强磁场打在竖直放置的荧光屏上．问：
（1）如果电子在t=0时刻进入偏转电场，则离开偏转电场时的侧向位移大小是多少？
（2）电子在刚穿出两板之间的偏转电场时最大侧向位移与最小侧向位移之比为多少？
（3）要使侧向位移最大的电子能垂直打在荧光屏上，匀强磁场的磁感应强度为多少？（已知电子的质量为m、电荷量为e）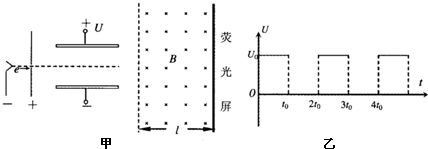
参考答案：（1）当电子在t=0时刻进入偏转电场时，侧向位移大小 为
y=12at20+vyt0=12πU0emdt20+U0emdt0?t0
得y=3U0et202dm
（2）由题意可知，要使电子的侧向位移最大，应让电子从0、2t0、4t0…等时刻进入偏转电场，在这种情况下，电子的侧向位移为
ymax=y=12at20+vyt0，
得 ymax=3U0et202dm
要使电子的侧向位移最小，应让电子从t0、3t0…等时刻进入偏转电场，在这种情况下，电子的侧向位移为
? ymin=12at20
解得，ymin=U0e2dmt20
所以最大侧向位移和最小侧向位移之比为ymax：ymin=3：1
（3）设电子从偏转电场中射出时的偏向角为θ，由于电子要垂直打在荧光屏上，所以电子在磁场中运动半径R，由几何关系有：
? R=lsinθ
设电子从偏转电场中出来时的速度为vt，垂直偏转极板的速度为vy，则电子从偏转电场中出来时的偏向角为：sinθ=vyvt
式中?vy=U0edmt0
又?R=mvtBe?
由上述四式可得：B=U0t0dl
答：（1）电子在t=0时刻进入偏转电场，则离开偏转电场时的侧向位移大小是3U0et202dm．
（2）电子从两平行板间射出时最大侧向位移与最小侧向位移之比是3：1．
（3）要使侧向位移最大的电子能垂直打在荧光屏上，匀强磁场的磁感应强度为U0t0dl．
本题解析：
本题难度：一般
4、选择题 一辆载重汽车在丘陵山地上匀速行驶，地形如图。由于车轮太陈旧，途中“放了炮”。你认为在途中A、B、C、D四处中，放炮的可能性最大的是
A．A处? B．B处 ?C．C处 ?D．D处
参考答案：C
本题解析：略
本题难度：简单
5、选择题 长l的轻杆一端固定着一个小球A，另一端可绕光滑水平轴O在竖直面内做圆周运动，如图所示，下面叙述符合实际的是（ ）
A．小球在最高点的速度至少为
| gl |
| gl |
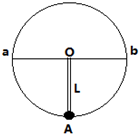
参考答案：A、杆可以表现为支持力，也可以表现为拉力，故小球在最高点的速度可以为零，故A错误；
B、在最高点，当球只受重力，时，根据牛顿第二定律，有：mg=mv2l，
解得：v=
本题解析：
本题难度：简单