时间:2018-10-13 00:39:11
1、实验题 某同学做“探究功与速度变化的关系”的实验，如图所示，小车在一条橡皮筋的作用下弹出沿木板滑行，这时橡皮筋对小车做的功为W．当用2条、3条…实验时，使每次实验中橡皮筋伸长的长度都保持一致，每次实验中小车获得的速度都由打点计时器所打的纸带测出。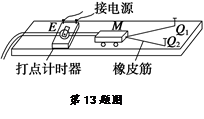
(1)除了图中已有的器材外，还需要导线、开关、交流电源和?(填测量工具)。?
(2)实验中小车会受到摩擦阻力，可以使木板适当倾斜来平衡摩擦力，需要在?(填“左”或“右”)侧垫高木板。
参考答案：（1）?刻度尺?；（2分）（2）?左?。（2分）
本题解析：本题考查的是“探究功与速度变化的关系”的实验相关问题，实验需要测量纸带上打的点之间的距离，故需要刻度尺；平衡摩擦力的方法让小车沿斜面向下的重力分力与摩擦阻力相等，小车可以匀速自由下滑，故在左边垫高；
本题难度：一般
2、选择题 一物体速度由0增加到v, 再从v增加到2v, 合外力做功分别为W1和W2，则W1和W2关系正确的是
A．W1=W2
B．W2=2W1
C．W2=3W1
D．W2=4W1
参考答案：C
本题解析：由动能定理，当物体速度由0增加到v,合力功为：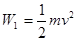
?，当从v增加到2v, 合外力做功：
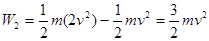，所以W2=3W1，选项C正确。，
本题难度：简单
3、简答题 如图所示，一根质量为m的金属棒MN水平放置在两根竖直的光滑平行金属导轨上，并始终与导轨保持良好接触，导轨间距为L，导轨下端接一阻值为R的电阻，其余电阻不计．在空间内有垂直于导轨平面的磁场，磁感应强度大小只随竖直方向y变化，变化规律B=ky，k为大于零的常数．质量为M=4m的物体静止在倾角θ=30°的光滑斜面上，并通过轻质光滑定滑轮和绝缘细绳与金属棒相连接．当金属棒沿y轴方向从y=0位置由静止开始向上运动h时，加速度恰好为0．不计空气阻力，斜面和磁场区域足够大，重力加速度为g．求：
（1）金属棒上升h时的速度；
（2）金属棒上升h的过程中，电阻R上产生的热量；
（3）金属棒上升h的过程中，通过金属棒横截面的电量．
参考答案：
（1）当金属棒的加速度为零时，Mgsin30°=F+mg?
库仑力：F=BIL=KhIL?
感应电流：I=BLvR=khLvR?
解以上方程得：v=mgRk2h2L2?
（2）设产生的焦耳热为Q，由能量的转化与守恒得：
12(M+m)v2=Mghsinθ-mgh-Q?
解得：Q=mgh-5m3g2R22k4L4h4?
（3）金属棒上升h的过程中，磁通量的变化：△Φ=.BLh=12kh?Lh=12kh2L
?流过金属棒截面的电量：q=.I?△t=.ER?△t?
?.E=△Φ△t?
解得：q=kh2L2R
答：（1）金属棒上升h时的速度v=mgRk2h2L2；
（2）金属棒上升h的过程中，电阻R上产生的热量mgh-5m3g2R22k4L4h4；
（3）金属棒上升h的过程中，通过金属棒横截面的电量kh2L2R．
本题解析：
本题难度：一般
4、选择题 总质量为M的列车，沿水平直线轨道匀速前进，其末节车厢质量为m，中途脱节，司机发觉时，机车已行驶L的距离，于是立即关闭油门，除去牵引力，如图所示。设运动的阻力与质量成正比，机车的牵引力是恒定的。当列车的两部分都停止时，它们的距离是多少？
参考答案：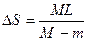
本题解析：此题用动能定理求解比用运动学、牛顿第二定律求解简便。
对车头，脱钩后的全过程用动能定理得：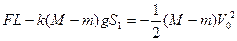
对车尾，脱钩后用动能定理得：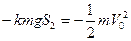
而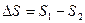
，由于原来列车是匀速前进的，所以F=kMg
由以上方程解得。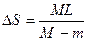
解二：假设末节车厢刚脱钩时，机车就撤去牵引力，则机车与末节车厢同时减速，因为阻力与质量成正比，减速过程中它们的加速度相同，所以同时停止，它们之间无位移差。事实是机车多走了距离L才关闭油门，相应的牵引力对机车多做了FL的功，这就要求机车相对于末节车厢多走一段距离△S，依靠摩擦力做功，将因牵引力多做功而增加的动能消耗掉，使机车与末节车厢最后达到相同的静止状态。所以有：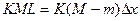
得△x=ML/(M－m)
本题难度：简单
5、填空题 A球的质量是B球质量的2倍，把它们竖直向上抛出，如果抛出时，人手对两球做的功相同，不考虑空气阻力，那么两球上升的最大高度之比hA：hB=______两球上升的时间之比tA：tB=______．
参考答案：对球，上升过程由动能定理得：
W-mgh=0-0，物体上升高度：h=Wmg，
两球上升的最大高度之比：
hAhB=WmAgWmBg=mBmA=mB2mB=12，
球做竖直上抛运动，上升时间与下降时间相等，
由位移公式得：h=12gt2，运动时间t=
本题解析：
本题难度：一般