时间:2018-10-13 00:18:41
1、计算题 如图12-16所示,横截面为矩形的管道中,充满了水银,管道的上下两壁为绝缘板,前后两壁为导体板(图中斜线部分),两导体板被一导线cd短路。管道的高度为a,宽度为b,长度为L。当加在管道两端截面上的压强差为P,水银沿管道方向自左向右流动时,作用在这段水银上的粘滞阻力f与速度成正比,即:f=kv.
(1)水银的稳定流速v1为多大?
(2)将管道置于一匀强磁场中,磁场与绝缘壁垂直,磁感应强度为B,方向向上,此时水银的稳定流速v2又是多大?(已知水银的电阻率为ρ,磁场只存在于管道所在的区域,不考虑管道两端之外水银对电路的影响。)
2、简答题 
试求:
金属棒MN运动达到稳定状态后,1s钟内外力F所做的功并说明能量的转化是否守恒.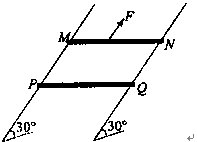
3、选择题 如图所示,一个闭合矩形金属线圈abcd从一定高度释放,且在下落过程中线圈平面始终在竖直平面上;在它进入一个有直线边界的足够大的匀强磁场的过程中,取线圈dc边刚进磁场时t=0,则描述其运动情况的图线可能是下图中的( )
A.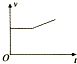
B.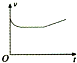
C.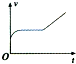
D.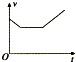
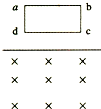
4、选择题 如图甲所示,光滑的平行导轨MN、PQ固定在水平面上,导轨表面上放着光滑导体棒ab、cd,两棒之间用绝缘细杆连接,两导体棒平行且与导轨垂直.现加一垂直导轨平面的匀强磁场,设磁场方向向下为正,磁感应强度B随时间t的变化规律如图乙所示,t1=2t0,不计ab、cd间电流的相互作用,不计导轨的电阻,每根导体棒的电阻为R,导轨间距和绝缘细杆的长均为L.下列说法正确的是(?)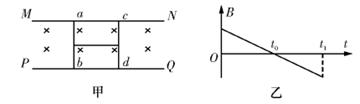
A.t= t0时轻杆既不被拉伸也不被压缩
B.在0~t1时间内,绝缘细杆先被拉伸后被压缩
C.在0~t1时间内,abcd回路中的电流方向是先顺时针后逆时针
D.若在0~t1时间内流过导体棒的电量为q,则t1时刻的磁感应强度大小为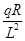
5、计算题 如图所示,在磁感应强度为B的水平方向的匀强磁场中竖直放置两平行导轨,磁场方向与导轨所在平面垂直。导轨上端跨接一阻值为R的电阻(导轨电阻不计)。两金属棒a和b的电阻均为R,质量分别为ma=2×10-2 kg和mb=1×10-2 kg,它们与导轨相连,并可沿导轨无摩擦滑动。闭合开关S,先固定b,用一恒力F向上拉,稳定后a以v1=10m/s的速度匀速运动,此时再释放b,b恰好保持静止,设导轨足够长,取g=10m/s2。
(1)求拉力F的大小;
(2)若将金属棒a固定,让金属棒b自由滑下(开关仍闭合),求b滑行的最大速度v2;
(3)若断开开关,将金属棒a和b都固定,使磁感应强度从B随时间均匀增加,经0.1s后磁感应强度增到2B时,a棒受到的安培力正好等于a棒的重力,求两金属棒间的距离h。