高中物理高考知识点《机械能守恒及其条件》高频考点预测（2018年最新版） - 高考物理题库

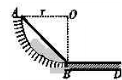
1、简答题如图2-12所示，一轻绳两端各系一小球（可视为质点），质量分别为M和m（M＞m）,跨放在一个光滑的半圆柱体上.两球从水平直径AB的两端由静止释放开始运动.当m刚好达到圆柱体侧面最高点C处时，恰脱离圆柱体.则两球质量之比M∶m=?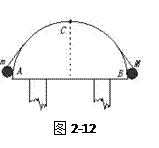

参考答案：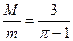

本题解析：选系统为研究对象，由机械能守恒定律得：
Mg·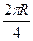=mgR+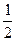（M+m）v2?①
因m到达最高点时恰离开圆柱体，据牛顿第二定律得：
mg=m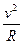?②
联立①②式得：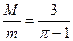

本题难度：一般

2、选择题如图所示，一均质杆长为?

r，从图示位置由静止开始沿光滑面ABD滑动，AB是半径为r的

1
4

圆弧，BD为水平面．则当杆滑到BD位置时的速度大小为（　　）
91考试网

A．

gr
2

B．

C．

2gr

D．2

参考答案：匀质直杆AB沿光滑轨道滑动过程中机械能守恒，
初态机械能E1=mg?r2，末态机械能E2=12mv2，
由E2=E1求得v=

本题解析：

本题难度：一般

3、选择题关于机械能守恒，下列说法正确的是
[? ]
A.做匀速直线运动的物体，其机械能一定守恒
B.做匀速圆周运动的物体，其机械能一定守恒
C.平抛运动的物体，其机械能一定守恒
D.物体不受摩擦力，机械能一定守恒

参考答案：C

本题解析：

本题难度：简单

4、选择题一小球以初速度v0竖直上抛，它能到达的最大高度为H，问下列几种情况中，哪种情况小球不可能达到高度H（忽略空气阻力）

[? ]

A．以初速v0沿光滑斜面向上运动（图a）
B．以初速v0沿光滑的抛物线轨道，从最低点向上运动（图b）
C．以初速v0沿半径为R的光滑圆轨道，从最低点向上运动（图c，H>R>H/2）
D．以初速v0沿半径为R的光滑圆轨道，从最低点向上运动（图d，R>H）

参考答案：C

本题解析：

本题难度：一般

5、选择题伽利略斜面理想实验使人们认识到引入能量概念的重要性。在此理想实验中，能说明能量在小球运动过程中不变的理由是
[? ]
A. 小球滚下斜面时，高度降低，速度增大
B. 小球滚上斜面时，高度增加，速度减小
C. 小球总能准确地到达与起始点相同的高度
D. 小球能在两斜面之间永不停止地来回滚动

参考答案：CD

本题解析：

本题难度：简单