时间:2018-10-11 00:40:45
1、选择题 如右图所示，有一半圆弧光滑轨道，半径为R，在与圆心等高的位置静止放置一个带正电的小球A，其质量为m，M、N之间有一方向水平向左的匀强电场，让小球A自由滚下进入匀强电场区域，水平面也是光滑的，下列说法正确的是( )
A．小球一定能穿过MN区域继续运动
B．如果小球没有穿过MN区域，小球一定能回到出发点
C．如果小球没有穿过MN区域，只要电场强度足够大，小球可以到达P点，且到达P点速度大于等于
D．如果小球一定能穿过MN区域，电场力做的功为
参考答案：B
本题解析：小球带正电，进入电场后做减速运动，如果小球达到N点还没有减速到零，说明小球穿过了MN区域，如果小球还没有到N点就减速为零，说明小球不能穿过MN区域，A项错．如果小球没有穿过MN区域，根据能量守恒定律，小球能回到出发点，且速度为零，B项对，C项错．如果小球一定能穿过MN区域，根据动能定理，电场力做的功与重力做的总功之和等于动能的变化，由于不知道小球在N点的速度是否为0，所以无法确定电场力做的功，D项错．
故选B
点评：带电粒子在电场中的运动，综合了静电场和力学的知识，分析方法和力学的分析方法基本相同．先分析受力情况再分析运动状态和运动过程（平衡、加速、减速，直 线或曲线），然后选用恰当的规律解题．解决这类问题的基本方法有两种，第一种利用力和运动的观点，选用牛顿第二定律和运动学公式求解；第二种利用能量转化 的观点，选用动能定理和功能关系求解．
本题难度：一般
2、选择题 如右图所示，在光滑绝缘的水平桌面上固定放置一光滑、绝缘的挡板ABCD，AB段为直线形挡板，BCD段是半径为R的圆弧形挡板， 挡板处于场强为E的匀强电场中，电场方向与圆直径MN平行．现有一带电荷量为q、质量为m的小球静止从挡板上的A点释放，并且小球能沿挡板内侧运动到D点抛出，则( )
A．小球运动到N点时，挡板对小球的弹力可能为零
B．小球运动到N点时，挡板对小球的弹力可能为Eq
C．小球运动到M点时，挡板对小球的弹力可能为零
D．小球运动到C点时，挡板对小球的弹力一定大于mg
参考答案：C
本题解析：小球沿光滑轨道内侧运动到D点抛出，说明小球在N、C、M点的速度均不为零，
对N点：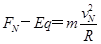
，
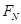必大于Eq，A、B均错误；
在C点：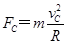 
，无法比较
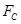与mg的大小，D错．C正确
故选C
点评：本题的关键是根据牛顿第二定律列出圆周运动向心力等式，根据等式分析
本题难度：一般
3、计算题 如图甲所示，
、
为水平放置的间距
的两块足够大的平行金属板，两板间有场强为
、方向由指向的匀强电场.一喷枪从、板的中央点
向水平线各个方向均匀地喷出初速度大小均为
的带电微粒.已知微粒的质量均为
、电荷量均为
，不计微粒间的相互作用、对板间电场和磁场的影响及空气阻力，取
.求：
（1）微粒落在金属板上所围成的图形面积.
（2）要使微粒不落在金属板上，通过计算说明如何调节两板间的场强.
（3）在满足（2）的情况下，在两板间加垂直于纸面向里的匀强磁场，磁感应强度
，调节喷枪使微粒可以向纸面内沿各个方向喷出（如图乙），求板被微粒打中的区域长度和微粒在磁场中运动的最短时间.
参考答案：（1）5.7m2（2）电场应该调节为方向向下，大小为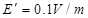
（3）0.1s
本题解析：（1）微粒在匀强电场做类平抛运动，油漆微粒的加速度: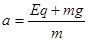 
①
根据运动学：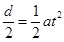
② 运动的半径：
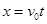③
落在B板上所形成圆形面积：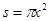
④
由①②③④式并代入数据得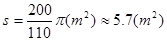
⑤
（2）要使微粒不落在金属板上，电场应反向，且有：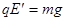
⑥
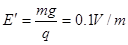⑦
故电场应该调节为方向向下，大小为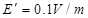
（3）微粒做匀速圆周运动，洛伦兹力充当向心力：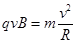
⑧ 
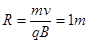⑨
竖直向下射出的微粒打在板的左端恰好与板相切，如图甲所示：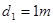
⑩
当粒子源和板右边击中点距离为直径时距离最远：如图乙所示：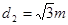
故板被微粒打中的区域的长度都为
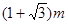
当粒子运动的圆弧轨迹最短时粒子运动的时间最短，故根据题意可知，当粒子恰好击中粒子源正下方的B板处时间最短， 如图丙所示：
微粒的运动周期：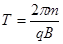 
根据距离和半径的关系可以知道对应的圆心角为60°，所以: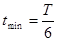
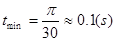
考点：带电粒子在匀强电场中的运动；带电粒子在匀强磁场中的运动；
本题难度：困难
4、计算题 如图所示，一质量为m、电量为q的带电粒子，以速度v沿平行于板面的方向射入电场中。极板间的电压为U，板长为L，板间距离为d。若不计带电粒子的重力，求带电粒子射出电场时
（1）侧向位移的大小
（2）速度的大小与方向
参考答案：
（1）
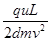（2）
，
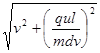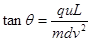
本题解析：略
本题难度：一般
5、选择题 如图所示，实线为某孤立点电荷产生的电场的几条电场线，虚线是某一带电粒子通过该电场区域的运动轨迹，a、b是轨迹上的两点。若带电粒子在运动中只受电场力的作用，下列说法中正确的是
参考答案：
本题解析：
本题难度：一般