时间:2018-10-11 00:39:37
1、选择题 多选
左端封闭、右端开口的粗细均匀的U形玻璃管,倒置时如图,其中斜线部分为水银。若此管保持竖直状态做自由落体运动,则与释放前相比( ? )

参考答案:BC
本题解析:
本题难度:一般
2、填空题 一定质量的气体处于某一平衡状态,此时其压强为p0,有人设计了四种途径,使气体经过每种途径后压强仍为p0.这四种途径中( )
A.先保持体积不变,降低压强,再保持温度不变,压缩体积
B.先保持体积不变,使气体升温,再保持温度不变,让体积膨胀
C.先保持温度不变,使体积膨胀,再保持体积不变,使气体升温
D.先保持温度不变,压缩气体,再保持体积不变,使气体降温
参考答案:ABCD
本题解析:此题考查气体的压强、体积、温度之间的关系以及微观上决定气体压强的因素.保持体积不变,降低压强,气体压强减小;再保持温度不变,压缩气体,体积变小,压强增大,A有可能.体积不变升温,压强变大,温度不变,体积膨胀,压强减小,B有可能.温度不变,体积膨胀,压强减小,体积不变,升温压强变大,C有可能.温度不变,压缩气体,压强增大,体积不变,降温,压强减小,D有可能.
本题难度:一般
3、简答题 1964年制成了世界上第一盏用海浪发电的航标灯.它的气室示意图如图所示,其工作原理是利用海浪上下起伏的力量将空气吸入气室,压缩后推入工作室,然后推动涡轮机带动发电机发电.当海水下降时阀门K1关闭,K2打开;吸入压强为1.0×105Pa的空气(可视为理想气体),吸气后气室中空气的总体积为0.8m3.当海水上升时K2立即关闭,海水推动活塞压缩吸入的空气,可以认为这一过程空气温度不变,当空气的体积被压缩到0.2m3时,阀门K1被推开,活塞继续推动空气使之进入工作室,同时工作室中的空气推动涡轮机工作,涡轮机带动发电机发电给航标灯提供电能,这一过程涡轮机带动发电机工作5s时间.
①试求阀门K1刚被推开时,气室内空气的压强;?
②若这一过程航标灯得到的功率为2.0×103W,涡轮机及发电机的总效率为80%,求空气对涡轮机所做的功.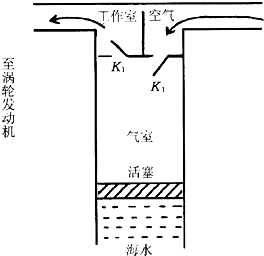
参考答案:①对于活塞内的气体,
P1=1.0×105Pa,V1=0.8m3,
P2=?V2=0.2m3,
由玻意耳定律得?P1V1=P2V2
所以 P2=P1V1V2=1.0×105×0.80.2Pa=4.0×105Pa,
②航标灯得到的功率为2.0×103W,即为输出的功率,涡轮机及发电机的总效率为80%,
所以空气对涡轮机所做的功 W=Ptη=2×103×50.8J=1.25×104J.
答:①阀门K1刚被推开时,气室内空气的压强为4.0×105Pa;
②空气对涡轮机所做的功为1.25×104J.
本题解析:
本题难度:一般
4、选择题 温度计是生活、生产中常用的测量装置。右图为一简易温度计,一根装有一小段有色水柱的细玻璃管穿过橡皮塞插入烧瓶内,封闭一定质量的气体。当外界温度发生变化时,水柱位置将上下变化。已知A、D间的测量范围为20℃—80℃,A、D间刻度均匀分布。由图可知,A、D及有色水柱下端所示温度分别为(?)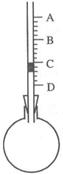
A、20℃、80℃、64℃? B、20℃、80℃、68℃
C、80℃、20℃、32℃? D、80℃、20℃、34℃
参考答案:C
本题解析:
本题难度:一般
5、填空题 如图,A,B是体积相同的气缸,B内有一导热的、可在气缸内无摩擦滑动的、体积不计的活塞C,D为不导热的阀门。起初,阀门关闭,A内装有压强p1=2.0×105a温度T1=300K的氮气。B内装有压强P2=1.0×105Pa,温度T2=600K的氧气。打开阀门D,活塞C向右移动,最后达到平衡,以V1和V2分别表示平衡后氮气和氧气的体积,则V1∶V2=______(假定氧气和氮气均为理想气体,并与外界无热交换,连接气缸的管道体积可忽略)
参考答案:4∶1
本题解析:
【错解分析】错解:开始是平衡状态,未态还是平衡状态,由理想气体状态方程可知:
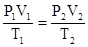 .
.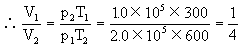
此题答案为1∶4。
理想气体状态方程或气体定律,针对的对象应为一定质量的理想气体,而不能是两种(或两部分)气体各自的状态,必须是一定质量的理想气体初、末两种状态之间满足的关系,上述解法把两部分气体的p1,p2,T1,T2与一定质量的气体前后两种状态的p1,p"1,T1,T"1混为一谈,以致出现完全相反的结论。
【正解】对于A容器中的氮气,其气体状态为:
p1=2.0×105pa? V1=V? T1=300K
P"1=P? V"1=V1(题目所设)? T"1=T
由气体状态方程可知: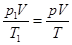 ?①
?①
对于B容器中的氧气,其气体状态为:
p2=1.0×105pa? V2=V? T2=600K
p"2=p? V"2=V2(题目所设)? T’2=T
由气态方程可知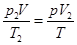 ?②
?②
联立①②消去T,V可得:
此题的正确答案为V1∶V2=4∶1
【点评】解决有关两部分气体相关联的问题时,要注意两方面的问题。首先,要把两部分气体分开看待,分别对每一部分气体分析出初、未状态的p,V,T情况,分别列出相应的方程(应用相应的定律、规律)切不可将两部分气体视为两种状态。
其次,要找出两部分气体之间的联系,如总体积不变,平衡时压强相等,等等。例如本题中,阀门关闭时两边气体体积相等,阀门打开两边气体压强相等,温度相等,利用这些关系,可以消去方程中的未知因素,否则,也解不出正确结果。
本题难度:一般