时间:2018-10-11 00:18:55
1、计算题 如图所示,轻弹簧的两端与质量均为2m的B、C两物块固定连接,静止在光滑水平面上,物块C紧靠挡板但不粘连.另一质量为m的小物块A以速度V0从右向左与B发生弹性正碰,碰撞时间极短可忽略不计.(所有过程都在弹簧弹性限度范围内)求: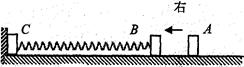
(1)A、B碰后瞬间各自的速度;
(2)弹簧第一次压缩最短与第一次伸长最长时弹性势能之比.
参考答案:(1)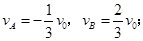 (2)
(2)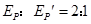
本题解析:(1)A、B发生弹性正碰,碰撞过程中,A、B组成的系统动量守恒、机械能守恒,以A、B组成的系统为研究对象,以A的初速度方向为正方向,由动量守恒定律得: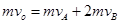 ,
,
在碰撞过程中机械能守恒,由机械能守恒定律得: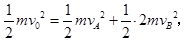 联立解得:
联立解得: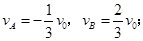
(2)弹簧第一次压缩到最短时,B的速度为零,该过程机械能守恒,由机械能守恒定律得,弹簧的弹性势能: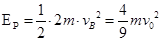 ,
,
从弹簧压缩最短到弹簧恢复原长时,B、C与弹簧组成的系统机械能守恒,弹簧恢复原长时,B的速度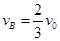 ,速度方向向右,C的速度为零,
,速度方向向右,C的速度为零,
从弹簧恢复原长到弹簧第一次伸长最长时,B、C与弹簧组成的系统动量守恒、机械能守恒,弹簧伸长最长时,B、C速度相等,以向右为正方向,由动量守恒定律得: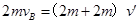 ,
,
由机械能守恒定律得: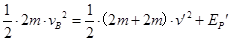 ,解得:
,解得: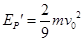 ,
,
弹簧第一次压缩最短与第一次伸长最长时弹性势能之比: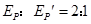 ;
;
考点:考查了机械能守恒,动量守恒,
本题难度:一般
2、选择题 从同一高度以相同的速率抛出质量相等的三个小球,分别做竖直上抛运动,竖直下抛运动,平抛运动,则它们从抛出到落地的过程,不计空气阻力,以下说法正确的是( )
A.运动的时间相等
B.加速度相同
C.落地时的速度相同
D.落地时的动能不相等
参考答案:B
本题解析:平抛运动在竖直方向上做自由落体运动,在同一高度自由落体运动的时间小于竖直上抛运动的时间,大于竖直下抛运动的时间,故A错误;竖直上抛运动、竖直下抛运动、平抛运动仅受重力,加速度都为g,故B正确;根据动能定理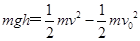 ,知初动能相等,高度相同,则末动能相等.末速度的大小相等,但方向不同,所以落地速度不同,故CD错误。
,知初动能相等,高度相同,则末动能相等.末速度的大小相等,但方向不同,所以落地速度不同,故CD错误。
考点:考查了抛体运动规律的应用
本题难度:一般
3、计算题 如图,一个倾角θ=30°的光滑直角三角形斜劈固定在水平地面上,顶端连有一轻质光滑定滑轮。质量为m的A物体置于地面,上端与劲度系数为k的竖直轻弹簧相连。一条轻质绳跨过定滑轮,一端与斜面上质量为m的B物体相连,另一端与弹簧上端连接。调整细线和A、B物体的位置,使弹簧处于原长状态,且细绳自然伸直并与三角斜劈的两个面平行。现将B物体由静止释放,已知B物体恰好能使A物体刚要离开地面但不继续上升。求: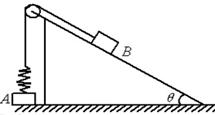
(1)B物体在斜面上下滑的最大距离x;
(2)B物体下滑到最低点时的加速度大小和方向;
(3)若将B物体换成质量为2m的C物体,C物体由上述初始位置静止释放,当A物体刚好要离开地面时,C物体的速度大小v。
参考答案:(1)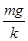 (2)
(2)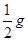 ;方向沿斜面向上;(3)
;方向沿斜面向上;(3)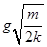
本题解析:(1)当A物体刚要离开地面但不上升时,A物体处于平衡状态,设B物体沿斜面下滑x,则弹簧伸长为x。
对A物体有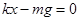 .........①
.........①
解得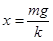 .......②
.......②
(2)当A物体刚要离开地面时,A与地面间作用力为0。 .................. ③
对A物体:由平衡条件得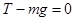 ....... ④
....... ④
设B物体的加速度大小为a,对B物体,由牛顿第二定律得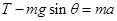 .......... ⑤
.......... ⑤
解得 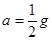 ...... ⑥
...... ⑥
B物体加速度的方向沿斜面向上.......⑦
(3)A物体刚要离开地面时,弹簧的弹性势能增加ΔE,对B物体下滑的过程,由能量守恒定律有: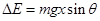 .........⑧
.........⑧
对C物体下滑的过程,由能量守恒定律有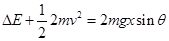 ..........⑨
..........⑨
解得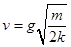 ...........⑩
...........⑩
考点:牛顿第二定律;能量守恒定律.
本题难度:困难
4、选择题 如图所示,将一质量为m的小球从空中o点以速度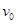 水平抛出,飞行一段时间后,小球经过P点时动能
水平抛出,飞行一段时间后,小球经过P点时动能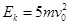 ,不计空气阻力,则小球从O到P( )
,不计空气阻力,则小球从O到P( )
A.下落的高度为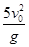
B.经过的时间为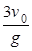
C.运动方向改变的角度为arctan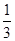
D.速度增量为3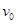 ,方向斜向下
,方向斜向下
参考答案:B
本题解析:小球在P点的动能:Ek=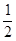 mvp2=
mvp2=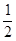 m(v02+vy2)=5mv02,解得:vy=3v0;故速度增量为3
m(v02+vy2)=5mv02,解得:vy=3v0;故速度增量为3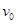 ,方向竖直向下; O和P点的高度差:
,方向竖直向下; O和P点的高度差: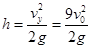 ;故选项AD错误;经过的时间满足竖直方向上的位移时间公式:h=
;故选项AD错误;经过的时间满足竖直方向上的位移时间公式:h=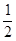 gt2,代入h解得:t=
gt2,代入h解得:t=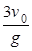 ;故选项B正确;设运动方向改变的角度为θ,知P点的速度方向与水平方向的夹角为θ,则:tanθ=
;故选项B正确;设运动方向改变的角度为θ,知P点的速度方向与水平方向的夹角为θ,则:tanθ=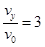 ,解得θ=arctan3,故选项C错误;故选:B.
,解得θ=arctan3,故选项C错误;故选:B.
考点:平抛运动的规律.
本题难度:一般
5、计算题 (18分)如图所示,一小锤用细线系于固定悬挂点O处,将小锤拉至O左侧一定高度(不超过O点所在的水平面)由静止释放,小锤恰好在最低点P与停在光滑水平面上的物块发生弹性正碰,碰后物块冲向右边固定在墙上的细长钢钉.
已知物块和小锤的质量分别为m、3m;物块和钢钉的长度分别为l、2l,OP距离为R;当小锤释放点距离P的高度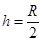 时,物块最终停止时其右端到墙的水平距离为
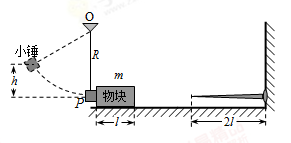
时,物块最终停止时其右端到墙的水平距离为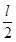 .重力加速度为g.物块未被穿透时受到的阻力大小只与钢钉进入物块的深度有关,物块被穿透后受到的阻力恒为
.重力加速度为g.物块未被穿透时受到的阻力大小只与钢钉进入物块的深度有关,物块被穿透后受到的阻力恒为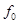 .
.
(1)当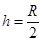 时,小锤与物块碰前瞬间对细线的拉力;
时,小锤与物块碰前瞬间对细线的拉力;
(2)当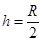 时,物块开始接触钢钉时的速度大小;
时,物块开始接触钢钉时的速度大小;
(3)要使物块最终被穿透但又没碰到墙,试求h的取值范围并讨论在此范围内物块停止时其右端与墙的水平距离x与h的关系式.
参考答案:(1)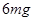 ,方向竖直向下;(2)
,方向竖直向下;(2)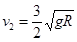 (3)
(3)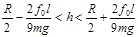 ,
,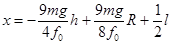
本题解析:(1)假设小锤下落h运动到P点时速度大小为 ,小锤与物块碰前瞬间受到细线的拉力大小为T,
,小锤与物块碰前瞬间受到细线的拉力大小为T,
小锤下降过程,应用动能定理有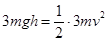 ①
①
小锤刚到P点,应用牛顿第二定律有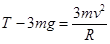 ②
②
当h=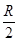 时,代入并联立①②解得
时,代入并联立①②解得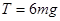 ③
③
由牛顿第三定律可知小锤与物块碰前瞬间对细线的拉力大小为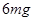 ,方向竖直向下;
,方向竖直向下;
(2)假设小锤与物块碰后速度大小分别为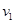 、
、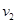 ,小锤与物块弹性碰撞过程应用动量守恒定律和机械能守恒定律有:
,小锤与物块弹性碰撞过程应用动量守恒定律和机械能守恒定律有: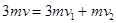 ④
④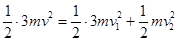 ⑤
⑤
当h=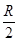 时,代入并联立①④⑤解得
时,代入并联立①④⑤解得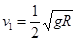 ,
, 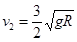 ⑥;
⑥;
(3)依题意可知,物块被穿透过程中受到的阻力为变力,假设此过程阻力做功为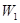 ;物块被穿透后运动过程所受阻力为恒力
;物块被穿透后运动过程所受阻力为恒力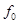 ,此过程阻力做功为
,此过程阻力做功为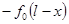 ;
;
物块减速到零的过程,由动能定理有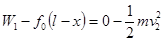 ⑦
⑦
当h=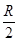 时,
时,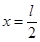 ,代入并联立⑥⑦解得
,代入并联立⑥⑦解得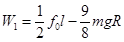 ⑧
⑧
当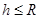 时,由前面分析可知物块接触钢钉前瞬间的速度为
时,由前面分析可知物块接触钢钉前瞬间的速度为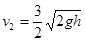 ,物块接触钢钉后到物块停止过程,代入并联立④⑤⑦⑧解得
,物块接触钢钉后到物块停止过程,代入并联立④⑤⑦⑧解得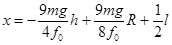 ⑨
⑨
依题意可知应满足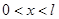
代入⑨可得: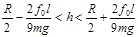 ⑩
⑩
题意又要求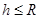 ,由
,由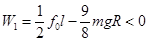 知
知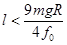 ,
,
代入⑩得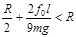 ,即⑩符合题意要求.
,即⑩符合题意要求.
综上,h的取值范围为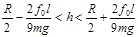 ,此范围内
,此范围内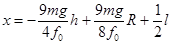 .
.
考点:本题考查动量守恒、动能定理
本题难度:一般