时间:2018-10-11 00:10:22
1、选择题 如图所示，在匀速转动的圆筒内壁上紧靠着一个物体与圆筒一起运动，物体相对桶壁静止则（ ）
A．物体受到3个力的作用
B．物体所受向心力是物体所受的重力提供的
C．物体所受向心力是物体所受的静摩擦力提供的
D．物体所受向心力是物体所受的桶壁的支持力提供的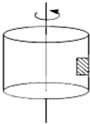
参考答案：A．对物体进行受力分析，物体在竖直方向上受重力和静摩擦力，并且这两个力相互平衡，水平方向受圆筒给它指向圆心的支持力，所以物体受到三个力作用，故A正确；
B．由A得分析可知物体的合外力即为圆筒给它指向圆心的支持力，所以物体所受向心力由支持力提供，故B错误；
C．由向心力的提供来源可知C错误；
D．由B可知D正确．
故选AD．
本题解析：
本题难度：一般
2、简答题 如图所示，在xOy坐标系中，第一象限存在一与xOy平面平行的匀强电场，在第二象限存在垂直于纸面的匀强磁场．在y轴上的P点有一静止的带正电的粒子，某时刻，粒子在很短时间内（可忽略不计）分裂成三个带正电的粒子1、2和3，它们所带的电荷量分别为q1、q2和q3，质量分别为m1、m2和m3，且q1：q2：q3=1：1：2，m1+m2=m3．带电粒子1和2沿x轴负方向进人磁场区域，带电粒子3沿x轴正方向进入电场区域．经过一段时间三个带电粒子同时射出场区，其中粒子1、3射出场区的方向垂直于x轴，粒子2射出场区的方向与x轴负方向的夹角为60°．忽略重力和粒子间的相互作用．求：
（1）三个粒子的质量之比；
（2）三个粒子进入场区时的速度大小之比；
（3）三个粒子射出场区时在x轴上的位移大小之比．
参考答案：（1）设粒子1、2在磁场中做匀速圆周运动的周期分别为T1和T2．则有
T1=2πr1v1=2πm1Bq1，
T2=2πr2v2=2πm2Bq2
由题意可知：14T1=16T2
所以m1m2=23
又因为m1+m2=m3
所以m1：m2：m3=2：3：5
（2）设粒子1、2在磁场中做匀速圆周运动的半径分别为r1和r2．则有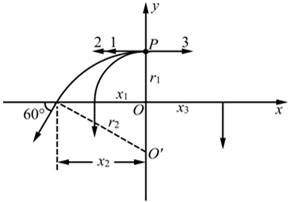
r1=m1v1Bq1那么：v1=r1Bq1m1
r2=m2v2Bq2?那么：v2=r2Bq2m2
由几何关系可知：r2=2r1
所以v1v2=34
在粒子分裂的过程中，动量守恒，则
m3v3-m1v1-m2v2=0
所以v1：v2：v3=15：20：18
（3）三个粒子射出场区时在x轴上的位移分别为x1、x2和x3．
由几何关系可知：
x1=r1，
x2=
本题解析：
本题难度：一般
3、选择题 如图所示，用长为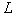
的细线拴一个质量为
的小球，使小球在水平面内做匀速圆周运动，细线与竖直方向间的夹角为
，关于小球的受力情况，下列说法错误的是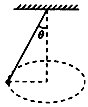
[? ]
A．小球受到重力、线的拉力和向心力三个力
B．向心力是细线的拉力和小球所受重力的合力
C．向心力等于细线对小球拉力的水平分量
D．向心力的大小等于
参考答案：A
本题解析：
本题难度：简单
4、简答题 质量为2吨的汽车在水平路面上做半径为40m的转弯，如果车速是36km/h，则：
（1）其所需的向心力多大？是由什么力提供的？
（2）若路面能提供的最大静摩擦力的值为车重的0.6倍，那么，若仍以36km/h速度转弯，转弯半径不小于多少m？
参考答案：（1）36km/h=10m/s
根据向心力公式得：Fn=mv2r=2000×10240=5000N，汽车转弯时，由静摩擦力提供向心力；
（2）根据题意知：最大静摩擦力fmax=0.6mg=0.6×20000=12000N，
根据向心力公式得：
fmax=mv2R
代入数据解得：R=16.7m
答：（1）其所需的向心力多大？是由什么力提供的？
（2）若路面能提供的最大静摩擦力的值为车重的0.6倍，那么，若仍以36km/h速度转弯，转弯半径不小于多少m？
本题解析：
本题难度：一般
5、简答题 如图所示，竖直平面内有一半?径R=0.9m、圆心角为60°的光滑圆弧?轨道PM，圆弧轨道最底端M处平滑?连接一长s=3m的粗糙平台MN，质?量分别为mA=4kg，mB=2kg的物块?A，B静置于M点，它们中间夹有长?度不计的轻质弹簧，弹簧与A连结，与B不相连，用细线拉紧A、B使弹簧处于压缩状态．N端有一小球C，用长为L的轻?绳悬吊，对N点刚好无压力．现烧断细线，A恰好能从P端滑出，B与C碰后总是交换速度．A、B、C均可视为质点，g取10m/s2，问：
（1）A刚滑上圆弧时对轨道的压力为多少？
（2）烧断细线前系统的弹性势能为多少？
（3）若B与C只能碰撞2次，B最终仍停在平台上，整个过程中绳子始终不松弛，求B与?平台间动摩擦因数?的范围及?取最小值时对应的绳长L．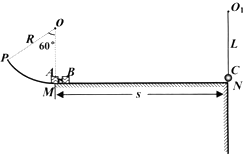
参考答案：（1）A在上滑过程中机械能守恒，有
12mv2A=mgR（1-cos60°）
vA=3m/s
根据牛顿运动定律?
N-mAg=mAv2AR
N=80N
由牛顿第三定律得，A对圆弧的压力为80N，方向竖直向下．
（2）由动量守恒得：
mAvA=mBvB
由能量守恒得
Ep=12mAv2A+12mBv2B
得：Ep=54J
（3）因B、C碰后速度交换，B静止，C做圆周运动，绳子不能松弛，一种情况是越过最高点，继续做圆周运动，
与B碰撞，B一定离开平台，不符合要求．另一种情况是C做圆周运动不超过14圆周，返回后再与B发生碰撞．?
B刚好能与C发生第一次碰撞
0-12mBv2B=-μmBgs
?解得?μ=0.6
?依题意有?μ＜0.6
B与C刚要发生第三次碰撞，则
0-12mBv2B=-3μmBgs
?解得?μ=0.2
?依题意有?μ＞0.2
B与C发生两次碰撞后不能从左侧滑出
0-12mBv2B=-2μmBgs-mBgR（1-cos60°）
解得?μ=0.225
?依题意有?μ≥0.225
综上所得?0.225≤μ＜0.6?
取μ=0.225，B与C碰撞后，C的速度最大，要绳不松弛，有：
12mBv2B1-12mBv2B=-μmBgs
vB1=vC
12mCv2C=mCgL
解得：L=1.125m
依题意：L≤1.125m
答：（1）A刚滑上圆弧时对轨道的压力为80N
（2）烧断细线前系统的弹性势能是54J
（3）若B与C只能碰撞2次，B最终仍停在平台上，整个过程中绳子始终不松弛，B与平台间动摩擦因数?的范围是?0.225≤μ＜0.6，
?取最小值时对应的绳L=1.125m．
本题解析：
本题难度：一般