时间:2018-10-10 23:49:13
1、简答题 从离地面80m的空中自由落下一个小球,g取10m/s2,求:
(1)经过多长时间落到地面?
(2)自开始下落计时,在第1s内的位移大小、最后1s内的位移大小;
(3)下落时间为总时间的一半时的位移大小和速度大小.
参考答案:(1)由h=12gt2
得物体下落到地面的时间为t=
本题解析:
本题难度:一般
2、选择题 一列车队从同一地点先后开出n辆汽车在平直的公路上排成直线行驶,各车均由静止出发先做加速度为a 的匀加速直线运动,达到同一速度v后改做匀速直线运动,欲使n辆车都匀速行驶时彼此距离均为s,则各辆车依次启动的时间间隔为(不计汽车的大小)
[? ]
A.
B.
C.
D.
参考答案:D
本题解析:
本题难度:一般
3、选择题 一质点做匀加速直线运动,第三秒内的位移2m,第四秒内的位移是2.5m,那么以下说法正确的是(?)
A.这两秒内平均速度是2.25m/s
B.第三秒末瞬时速度是2.5m/s
C.质点的加速度是0.125m/s2
D.质点的加速度是0.25m/s2
参考答案:A
本题解析:本题考查匀变速直线运动的规律
两秒内平均速度是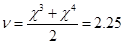 ?m/s;第三秒末瞬时速度等于这两秒内的平均速度;质点的加速度
?m/s;第三秒末瞬时速度等于这两秒内的平均速度;质点的加速度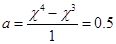 ?m/s2
?m/s2
本题关键是平均速度和加速度的求法
本题难度:一般
4、选择题 如图所示,小球从竖直砖墙某位置静止释放做初速为零的匀加速直线运动,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的位置.连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中的信息,下列判断正确的是( )
A.位置“1”是小球释放的初始位置
B.小球在位置“3”的速度大小为
| 7d 2T |
| d T2 |
| 11d 2T |
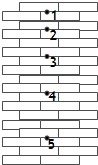
参考答案:由图可知1、2之间的距离为H1=2d,2、3之间的距离为H2=3d,3、4之间的距离为H3=4d,4、5之间的距离为H4=5d.
由于△H=H4-H3=H3-H2=H2-H1=d
即在连续相等的时间内物体的位移差等于恒量,
故根据△H=aT2可得
物体的加速度a=△HT2=dT2
故C正确.
若位置“1”是小球释放的初始位置,则有H1=12at12=12a?T2
H2=12a?t22=12a(2T)2
故有H1H2=14
显然与已知相矛盾,故位置“1”不是小球释放的初始位置.
故A错误.
因为位置“3”所处的时刻是位置“2”和位置“4”所处的时刻的中点时刻,
故v3=H242T=7d2T
故B正确.
根据vt=v0+at
可得小球在位置“5”的速度大小为
v5=v3+at=7d2T+dT2×2T=11d2T
故D正确.
故选B、C、D.
本题解析:
本题难度:一般
5、计算题 (6分)一辆汽车在平直的公路上做匀变速直线运动,该公路每隔60米就有一电线杆,汽车通过第一根和第二根电线杆用了5秒,通过第二根和第三根电线杆用了3秒。求:汽车的加速度和经过第一根电线杆时的瞬时速度。
参考答案: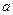 =2m/s2?
=2m/s2?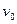 =7m/s
=7m/s
本题解析:由运动学公式得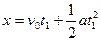 ①?(2分)
①?(2分) ②?(2分)
②?(2分)
将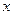 ="60m?"
="60m?" 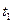 ="5s?"
="5s?" 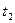 =8s代入①②得:
=8s代入①②得: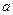 =2m/s2?
=2m/s2?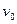 ="7m/s?" ?(2分)
="7m/s?" ?(2分)
本题难度:简单