时间:2018-10-02 05:04:29
1、计算题 如图所示为一种质谱仪示意图，位于A处电荷量为q、质量为m的离子（重力不计），从静止开始经加速电场加速后沿图中虚线做匀速圆周运动通过静电分析器，再由P点进入磁分析器后，最终打在乳胶片上的Q点。已知静电分析器通道的半径为R，均匀辐射电场的场强为E磁分析器中有垂直纸面向外的匀强磁 场，磁感应强度为B。求：
(1)离子在静电分析器中做匀速圆周运动的速度大小；
(2)加速电场的电压U；
(3)P，Q两点间的距离。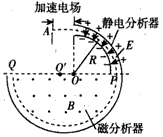
参考答案：解：(1)离子在辐向电场中做匀速圆周运动，有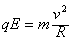 
，所以
(2)离子在加速电场中加速，根据动能定理有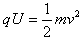
，所以
(3)离子在匀强磁场中做匀速圆周运动，洛伦兹力提供向心力，有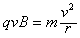
（或
所以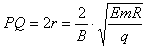
本题解析：
本题难度：困难
2、计算题 在某回旋加速器中，磁场的磁感应强度为B，粒子源射出的粒子质量为m，电荷量为q，粒子的最大回旋半径为Rm，问：
(1)D形盒内有无电场？
(2)粒子在盒内做何种运动？
(3)所加交变电场的周期是多大？
(4)粒子离开加速器时能量是多大？
(5)设两D形盒间电场的电势差为U，盒间距离为d，其间电场均匀，求把静止粒子加速到上述能量所需的时间。
参考答案：解：(1)D形盒由金属导体制成，具有屏蔽外电场的作用，盒内无电场
(2)带电粒子在盒内做匀速圆周运动，每次加速后轨道半径增大
(3)交变电场的周期应与粒子旋转的周期相同，即
(4)粒子离开加速器时达到最大速度vm，由
，可得vm=
则其动能为
(5)设粒子达到最大动能须经n次加速，则粒子在回旋加速器中运动的时间t应为在D形盒内的回旋时间t1与通过D形盒间的缝隙的加速时间t2之和，即t=t1+t2
由nqU=Ekm，得n
则粒子旋转的周期数为粒子在两D形盒缝隙中加速时，受到的电场力为
，运动的加速度
，质子n次通过缝隙的总位移为s=nd，由于质子n次加速的过程可视为初速度为零的匀加速直线运动，故有（注意等效的思想方法） 
所以
本题解析：
本题难度：困难
3、选择题 如图所示是粒子速度选择器的原理图，如果粒子所具有的速率v=E/B那么（ ）
A．带正电粒子必须沿ab方向从左侧进入场区，才能沿直线通过
B．带负电粒子必须沿ba方向从右侧进入场区，才能沿直线通过
C．不论粒子电性如何，沿ab方向从左侧进入场区，都能沿直线通过
D．不论粒子电性如何，沿ba方向从右侧进入场区，都能沿直线通过
参考答案：AC
本题解析：
本题难度：简单
4、选择题 一个用于加速质子的回旋加速器，其核心部分如图所示，D形盒半径为R，垂直D形盒底面的匀强磁场的磁感应强度为B，两盒分别与交流电源相连．下列说法正确的是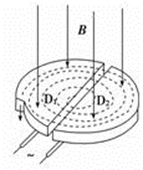
A．质子被加速后的最大速度随B、R的增大而增大
B．质子被加速后的最大速度随加速电压的增大而增大
C．只要R足够大，质子的速度可以被加速到任意值
D．为了使质子每次经过D形盒间缝隙时都能得到加速，应使交变电压的周期等于质子的回旋周期
参考答案：AD
本题解析：粒子在磁场中运动时，洛伦兹力提供向心力，满足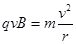
，则
，由此可知质子的最大速度只与粒子本身的荷质比，加速器半径，和磁场大小有关，与加速电压无关，当r=R时，vm最大，质子被加速后的最大速度随B、R的增大而增大，与加速的电压无关，A选项正确，B、C选项错误；运动周期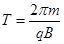
（电场中加速时间忽略不计）,故使交变电压的周期等于质子的回旋周期，D选项正确。理解回旋加速器工作原理，熟练运用相关公式，便可解出此题。
本题难度：简单
5、计算题 在高能物理研究中，粒子回旋加速器起着重要作用，如图甲为它的示意图。它由两个铝制D型金属扁盒组成，两个D形盒正中间开有一条窄缝。两个D型盒处在匀强磁场中并接有高频交变电压。图乙为俯视图，在D型盒上半面中心S处有一正离子源，它发出的正离子，经狭缝电压加速后，进入D型盒中。在磁场力的作用下运动半周，再经狭缝电压加速。如此周而复始，最后到达D型盒的边缘，获得最大速度，由导出装置导出。已知正离子的电荷量为q，质量为m，加速时电极间电压大小为U，磁场的磁感应强度为B，D型盒的半径为R。每次加速的时间很短，可以忽略不计。正离子从离子源出发时的初速度为零，求
（1）为了使正离子每经过窄缝都被加速，求交变电压的频率；
（2）求离子能获得的最大动能；
（3）求离子第1次与第n次在下半盒中运动的轨道半径之比。
参考答案：解：（1）使正离子每经过窄缝都被加速，交变电压的频率应等于离子做圆周运动的频率正离子在磁场中做匀速圆周运动，由洛仑兹力提供向心力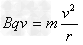
又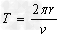
解得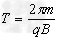
?
所以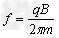
?
（2）当离子从D盒边缘离开时速度最大，此时离子做圆周运动的半径为D盒的半径有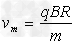
离子获得的最大动能为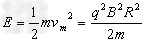
（3）离子从S点经电场加速1次后，以速度v1第1次进入下半盒
由动能定理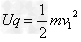
解得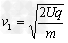
，
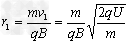
离子从S点经电场加速3次后，以速度v3第2次进入下半盒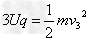
解得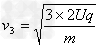
，
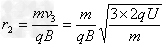
离子经电场加速（2n－1）次后，第n次进入磁场
同理可得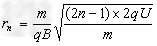
所以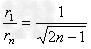 
（n = 1，2，3 ……）
本题解析：
本题难度：困难