时间:2018-10-02 04:52:57
1、选择题 质点做匀速圆周运动,下列物理量中不变的是( )
A.线速度
B.角速度
C.向心加速度
D.周期
参考答案:BD
本题解析:速度、向心力、加速度是矢量,有大小有方向,要保持不变,大小和方向都不变.在匀速圆周运动的过程中,速度的方向时刻改变,加速度、向心力的方向始终指向圆心,所以方向也是时刻改变.角速度不变,周期没有方向也不变.故选BD
考点:考查了匀速圆周运动
点评:解决本题的关键知道匀速圆周运动的过程中,速度的大小、向心力的大小、向心加速度的大小保持不变,但方向时刻改变.
本题难度:一般
2、计算题 我国月球探测计划“嫦娥工程”已经启动,科学家对月球的探索会越来越深入。
(1)若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,月球绕地球的运动近似看做匀速圆周运动,试求出月球绕地球运动的轨道半径;
(2)若宇航员随登月飞船登陆月球后,在月球表面高度为h的某处以速度v0水平抛出一个小球,小球飞出的水平距离为x。已知月球半径为R月,引力常量为G,试求出月球的质量M月。
参考答案:(1) 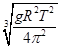 (2)
(2)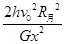
本题解析:(1)设地球质量为M,月球质量为M月,根据万有引力定律及向心力公式得: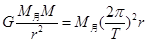 .............①
.............①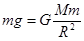 .........②
.........②
解得: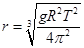 ...... ③
...... ③
(2)设月球表面处的重力加速度为g月,小球飞行时间为t, 根据题意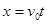 ....... ④
....... ④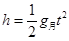 ........... ⑤
........... ⑤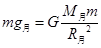 .......... ⑥
.......... ⑥
解得:.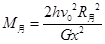 ........ ⑦
........ ⑦
考点:万有引力定律的应用.
本题难度:困难
3、计算题 如图所示,BC为半径等于 竖直放置的光滑细圆管,O为细圆管的圆心,BO与竖直线的夹角为45°;在圆管的末端C连接一光滑水平面,水平面上一质量为M=1.5kg的木块与一轻质弹簧拴接,轻弹簧的另一端固定于竖直墙壁上。现有一质量为m=0.5kg的小球从O点正上方某处A点以v0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始即受到始终竖直向上的恒力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失。小球过后与木块发生完全非弹性碰撞(g=10m/s2)。求:
竖直放置的光滑细圆管,O为细圆管的圆心,BO与竖直线的夹角为45°;在圆管的末端C连接一光滑水平面,水平面上一质量为M=1.5kg的木块与一轻质弹簧拴接,轻弹簧的另一端固定于竖直墙壁上。现有一质量为m=0.5kg的小球从O点正上方某处A点以v0水平抛出,恰好能垂直OB从B点进入细圆管,小球从进入圆管开始即受到始终竖直向上的恒力F=5N的作用,当小球运动到圆管的末端C时作用力F立即消失。小球过后与木块发生完全非弹性碰撞(g=10m/s2)。求:
小题1:小球在A点水平抛出的初速度v0;
小题2:小球在圆管运动中对圆管的压力N;
小题3:弹簧的最大弹性势能EP。
参考答案:
小题1: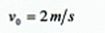
小题2: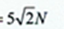
小题3:
本题解析:
本题难度:一般
4、计算题 质量m=2×103kg,汽车以 的速度通过某凸形桥的最高点时,受到桥面的支持力N=1.5×104N,取g=10m/s2,则桥面的半径为多少?当车速
的速度通过某凸形桥的最高点时,受到桥面的支持力N=1.5×104N,取g=10m/s2,则桥面的半径为多少?当车速 为多大时,车在桥最高点时对桥面的压力恰好为零?
为多大时,车在桥最高点时对桥面的压力恰好为零?
参考答案:①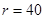 m?②
m?② ="20" m/s
="20" m/s
本题解析:对车受力分析如图所示,
(1)设桥面的半径为r,由向心力公式可知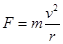 ;?(2分)
;?(2分)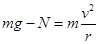 ?(3分)
?(3分)
代入数据解得?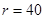 m?(2分)
m?(2分)
(2)车在桥最高点时对桥面的压力恰好为零时有?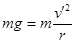 ? (3分)
? (3分)
代入数据解得? ="20" m/s?(2分)
="20" m/s?(2分)
本题难度:简单
5、计算题 如图所示,水平轨道上轻弹簧左端固定,弹簧处于自然状态时,其右端位于P点,现用一质量m=0.1 kg的小物块(可视为质点)将弹簧压缩后释放,物块经过P点时的速度v0=6 m/s,经过水平轨道右端Q点后恰好沿半圆光滑轨道的切线进入竖直固定的圆轨道,最后物块经轨道最低点A抛出后落到B点,若物块与水平轨道间的动摩擦因数μ=0.15,s=4 m,R=1 m,A到B的竖直高度h=1.25 m,取g=10 m/s2.
(1)求物块到达Q点时的速度大小(保留根号).
(2)判断物块经过Q点后能否沿圆周轨道运动.简单说明理由。
(3)若物块从A水平抛出的水平位移大小为4 m,求物块在A点时对圆轨道的压力.
参考答案:(1) ?
?
(2)物块能经过Q点沿圆周轨道运动?(3)? FN=7.4N
本题解析:⑴物块由P---Q:? a=-μg? ?
?
得: ?
?
(2)由于vt> =
= m/s,所以 物块能经过Q点沿圆周轨道运动 (3)物块A---B:? X=vA.t?
m/s,所以 物块能经过Q点沿圆周轨道运动 (3)物块A---B:? X=vA.t?
H= ?
?
得: ?
?
A点, ?
?
FN=7.4N?
由牛顿第三定律知:物块在A点对轨道的压力为7.4N,方向竖直向下。
本题难度:一般