时间:2018-10-02 04:05:44
1、选择题 如图所示,M、N为两块水平放置的平行金属板,距平行板右端L处有竖直屏,平行板长、板间距也均为L,板间电压恒定。一带电粒子(重力不计)以平行于板的初速度v0沿两板中线进入电场,粒子在屏上的落点距O点的距离为 。当分布均匀的大量上述粒子均以平行于板的初速度v0从MN 板左端各位置进入电场(忽略粒子间相互作用),下列结论正确的是
。当分布均匀的大量上述粒子均以平行于板的初速度v0从MN 板左端各位置进入电场(忽略粒子间相互作用),下列结论正确的是
[? ]
A.有 的粒子能到达屏上
的粒子能到达屏上
B.有 的粒子能到达屏上
的粒子能到达屏上
C.有 的粒子能到达屏上
的粒子能到达屏上
D.有 的粒子能到达屏上
的粒子能到达屏上
参考答案:B
本题解析:
本题难度:一般
2、选择题 一带电油滴在匀强电场E中的运动轨迹如图中虚线所示,电场方向竖直向下.若不计空气阻力,则此带电油滴从a运动到b的过程中,能量变化情况为( )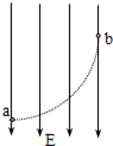
A.动能减小
B.电势能增加
C.重力势能和电势能之和增加
D.动能和电势能之和减小
参考答案:D
本题解析:带电油滴的运动轨迹为曲线,则它受到的电场力与重力的合力方向指向曲线的凹面,故电场力与重力的合力方向斜向上,粒子由a运动到b时,位移方向与合力方向的夹角小于90°,合力做正功,故由动能定理可知粒子的动能增加,A错误;又由于粒子的重力势能、电势能与动能之和是不变的,故粒子的重力势能和电势能之和减小,C错误;又因为其重力势能在增大,故动能与电势能之和会减小,D正确。
考点:粒子在电场、重力场的复合场中的运动情况。
本题难度:困难
3、计算题 如图所示,在平面直角坐标系xOy内,第Ⅰ象限有沿-y方向的匀强电场,第Ⅳ象限有垂直于纸面向外的匀强磁场.现有一质量为m、带电量为+q的粒子(重力不计)以初速度v0沿-x方向从坐标为(3l,l)的P点开始运动,接着进入磁场后由坐标原点O射出,射出时速度方向与y轴方向夹角为45°,求:
(1)粒子从O点射出时的速度v;
(2)电场强度E的大小;
(3)粒子从P点运动到O点所用的时间.
参考答案:(1) v=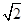 v0?(2) E=
v0?(2) E=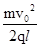 ?(3) T=t1+t2=(2+
?(3) T=t1+t2=(2+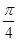 )
)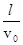
本题解析:(1)带电粒子在电场中做类平抛运动,进入磁场后做匀速圆周运动,最终由O点射出.(如图)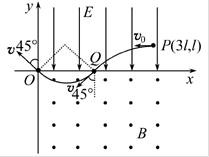
根据对称性可知,粒子在Q点时的速度大小与粒子在O点的速度大小相等,均为v,方向与-x轴方向成45°角,则有?
vcos45°=v0?(2分)?解得v=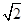 v0?
v0?
(2)在P到Q过程中,由动能定理得
qEl=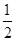 mv2-
mv2-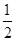 m
m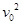 ?解得E=
?解得E=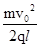 ?
?
(3)设粒子在电场中运动的时间为t1,则l=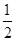 a
a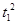 =
=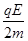
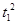 ?
?
设粒子在磁场中做匀速圆周运动的半径为r,由几何关系得 =3l-v0t1?
=3l-v0t1?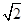 r=
r= ?
?
粒子在磁场中的运动时间为? t2=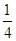 ×
×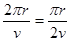 ?
?
由以上各式联立求得粒子在由P到O过程中的总时间为T=t1+t2=(2+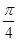 )
)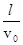 ?
?
点评:带电粒子在电场中的运动,综合了静电场和力学的知识,分析方法和力学的分析方法基本相同.先分析受力情况再分析运动状态和运动过程,然后选用恰当的规律解题.解决这类问题的基本方法有两种,第一种利用力和运动的观点,选用牛顿第二定律和运动学公式求解;第二种利用能量转化的观点,选用动能定理和功能关系求解.
本题难度:一般
4、计算题 如图所示为研究电子枪中电子在电场中运动的简化模型示意图。在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场I和II,两电场的边界均是边长为L的正方形(不计电子所受重力)。若在该区域AB边的中点处由静止释放质量为m,带电量为e的电子: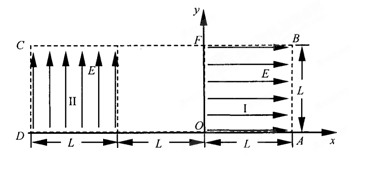
(1)求电子离开匀强电场I时的速度;
(2)求电子离开匀强电场II的位置(位置坐标用L表示)
参考答案: (1) 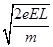 ;(2)(-2L,
;(2)(-2L,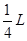 )
)
本题解析:
试题分析:(1)电子在区域Ⅰ中运动时,由动能定理得:
eEL=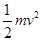 得:v=
得:v=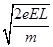
(2)电子从CD区域右侧中点进入区域Ⅲ匀强电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动.设电子的质量为m,电量为e,假设电子从CD边射出,出射点纵坐标为y,匀变速直线运动公式有: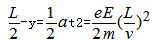
解得:y=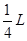 ,所以原假设成立,即电子离开ABCD区域的位置坐标为(-2L,
,所以原假设成立,即电子离开ABCD区域的位置坐标为(-2L,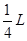 )
)
考点:带电粒子在匀强电场中的运动;平抛运动
本题难度:一般
5、计算题 (10分)如图所示,水平放置的两块长直平行金属板a、b相距d=0.10m,a、b间的电场强度为E=5.0×105N/C,b板下方整个空间存在着磁感应强度大小为B=6.0T、方向垂直纸面向里的匀强磁场.今有一质量为m=4.8×10-25kg、电荷量为q=1.6×10-18C的带正电的粒子(不计重力),从贴近a板的左端以v0 =1.0×106m/s的初速度水平射入匀强电场,刚好从狭缝P处穿过b板而垂直进入匀强磁场,最后粒子回到b板的Q处(图中未画出).求:
(1)粒子从狭缝P处穿过b板进入匀强磁场的速度大小和方向θ.
(2)P、Q之间的距离L.
参考答案:(1)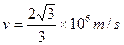 ? θ=300(2)L=5.8cm
? θ=300(2)L=5.8cm
本题解析:(10分)
(1)?粒子从a板左端运动到P处,由动能定理得
 --------------------(2分)
--------------------(2分)
代入有关数据,解得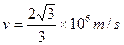 ---------------(1分)
---------------(1分) ,代入数据得θ=300 --------------------- (2分)
,代入数据得θ=300 --------------------- (2分)
(2)粒子在磁场中做匀速圆周运动,圆心为O,半径为r,如图,由几何关系得 --------------------- (1分),又
--------------------- (1分),又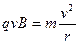 -------------------(1分)
-------------------(1分)
联立求得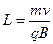 --------------(1分)?代入数据解得L=5.8cm--------------(2分)
--------------(1分)?代入数据解得L=5.8cm--------------(2分)
本题难度:一般