时间:2018-10-01 02:02:02
1、填空题 在某次足球比赛中,以10m/s向左做直线运动的足球,被某一运动员飞起一脚,足球在0.2s内速度大小改变为20m/s反向飞出,若足球在这段时间内做匀变速运动,则足球的加速度大小为______m/s2,方向为______.
参考答案:规定向左为正方向,
根据加速度的公式a=△v△t得
a=-20-100.2m/s2=-150m/s2.
负号表示加速度的方向与正方向相反,即向右.
故答案为:150,向右.
本题解析:
本题难度:简单
2、选择题 一薄圆盘可绕通过圆盘中心且垂直于盘面的竖直轴OO′转动,在圆盘上放置一小木块.当圆盘匀速转动时,木块相对圆盘静止.关于木块以下说法正确的是( )
A.由于木块相对圆盘静止,所以不受摩擦力
B.由于木块运动,所以受到与运动方向相反的滑动摩擦力
C.木块受到圆盘对它的静摩擦力,方向指向圆盘中心
D.由于木块做匀速圆周运动,所以,除了受到重力、支持力、摩擦力外,还受向心力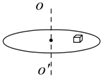
参考答案:
以小木块为研究对象,受力如图所示,木块相对圆盘静止,与圆盘一起做匀速圆周运动,小木块做匀速圆周运动需要的向心力在水平面内指向圆心,重力G与支持力FN在竖直方向上,G与FN不可能提供向心力,因此小木块作圆周运动的向心力由静摩擦力f提供.
故选C.
本题解析:
本题难度:一般
3、填空题 在“测定匀变速直线运动的加速度”的实验中,打点计时器交流电的频率为50Hz,某同学的实验纸带如图所示,取其中清晰地点O开始每打五个点取一个计数点标为A、B、C、D,则纸带中相邻两计数点间的时间为______s,在打出A、D两点的时间间隔中,纸带运动的平均速度是______m/s,B点的瞬时速度vB=______m/s.纸带的加速度a=______m/s2.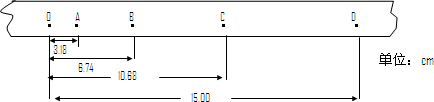
参考答案:每打五个点取一个计数点,又因打点计时器每隔0.02s打一个点,所以相邻两计数点间的时间T=0.1s.
.vAD=xAD3T=(15.00-3.18)×10-23×0.1m/s=0.394m/s
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上B点时小车的瞬时速度大小;
vB=xAC2T=(10.68-3.18)×10-22×0.1m/s=0.375m/s
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x3-x1=2a1T2?
x4-x2=2a2T2?
?为了更加准确的求解加速度,我们对两个加速度取平均值
得:a=12(a1+a2)
即小车运动的加速度计算表达式为:a=x4+x3-x2-x14T2
a=xBD-xOB4T2m/s2=0.38m/s2
故答案为:0.1;0.394;0.375;0.38
本题解析:
本题难度:一般
4、选择题 如图所示,圆锥摆甲乙的摆长之比为2:1,两摆球的质量相同,今使两圆锥摆做顶角分别为30°、60°的圆锥摆运动,则( )
A.两摆球的向心加速度之比为1:3
B.两圆锥摆的运动周期之比为2:1
C.摆球的线速度之比为1:1
D.摆球的角速度之比为1:2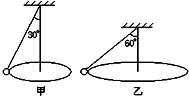
参考答案:解;小球在水平面内做匀速圆周运动,对小球受力分析,如图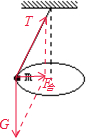
设细线与竖直方向的夹角为θ,r=Lsinθ,F合=mgtanθ,L1=2L2
根据牛顿第二定律得:a=F合m=gtanθ,所以两摆球的向心加速度之比为tan30°tan60°=13,故A正确;
根据向心力公式F合=mv2r得:摆球的线速度之比为
本题解析:
本题难度:简单
5、简答题 如图,真空室内竖直条形区域I存在垂直纸面向外的匀强磁场,条形区域Ⅱ(含I、Ⅱ区域分界面)存在水平向右的匀强电场,电场强度为E,磁场和电场宽度均为L且足够长,M、N为涂有荧光物质的竖直板.现有一束质子从A处连续不断地射入磁场,入射方向与M板成60°夹角且与纸面平行,质子束由两部分组成,一部分为速度大小为v的低速质子,另一部分为速度大小为3v的高速质子,当I区中磁场较强时,M板出现两个亮斑,缓慢改变磁场强弱,直至亮斑相继消失为止,此时观察到N板有两个亮斑.已知质子质量为m,电量为e,不计质子重力和相互作用力,求:
(1)此时I区的磁感应强度;
(2)到达N板下方亮斑的质子在磁场中运动的时间;
(3)N板两个亮斑之间的距离.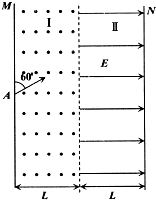
参考答案:(1)此时低速质子速度恰好与两场交界相切且与电场方向垂直,在磁场中运动半径为R1
?evB=mv2R1?①
?R1+R1cos60°=L?②
由①②得?B=3mv2eL?③
(2)低速质子在磁场中运动时间?t=2πR13v?④
由②④得?t=4πL9v?⑤
(3)高速质子轨道半径?R2=3R1?⑥
由几何关系知此时沿电场线方向进入电场,到达N板时与A点竖直高度差
h1=R2(1-sin60°)?⑦
低速质子在磁场中偏转距离
?h2=R1sin60°?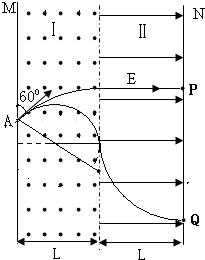
?⑧
在电场中偏转距离
h3=vt′⑨
在电场中时间?t′,L=12at′2?⑩
?eE=ma?(11)
由②⑥⑦⑧⑨⑩(11)得
亮斑PQ间距?h=h1+h2+h3=(2-2
本题解析:
本题难度:一般